La scrittura Latex rappresenta essenzialmente un linguaggio matematico, basato su simboli e formule algebriche-matematiche. Il Latex permette di fornire una rappresentazione dell’algoritmo maggiormente visibile dal punto di vista estetico e formale. In altre parole, entrando nello specifico, possiamo dire che il Latex è un programma di composizione tipografica open-source.
Prima di iniziare a dare la rappresentazione delle varie funzioni, bisogna ricordare che ogni funzione per essere correttamente utilizzata deve essere preceduta e posticipata dal segno del dollaro $.
FRAZIONI
\frac{numeratore}{denominatore}
ESEMPIO
$\frac{x-1}{x+3}$
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\frac{x-1}{x+3}$
INDICE
variabile_{indice}
ESEMPIO
x^3
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$x^3$
POTENZE
base^{argomento}
ESEMPIO
3^{2x}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$3^{2x}$
RADICALI
\sqrt[indice di radice]{radicando}
ESEMPIO
\sqrt[3]{4x^2+2x}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\sqrt[3]{4x^2+2x}$
RADICE QUADRATA
\sqrt {radicando}
ESEMPIO
\sqrt {x^3-y^2}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\sqrt {x^3-y^2}$
LIMITI
\lim_{variabile\to valore}{argomento del limite}
ESEMPIO
\lim_{x\to 1}{3x+3^x}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\lim_{x\to 1}{3x+3^x}$
LOGARITMI
\log_{base}{argomento}
ESEMPIO
\log_{10}{\ln x + 2}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\log_{10}{\ln x + 2}$
DERIVATE
\frac {d}{dx}\left (funzione\right)
ESEMPIO
\frac {d}{dx}\left (\frac{x-1}{x+3} \right)
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\frac {d}{dx}\left (\frac{x-1}{x+3} \right)$
INTEGRALI
\int{estremo basso}^{estremo alto}{integranda}
ESEMPIO
\int{a}^{b}{x dx}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\int{a}^{b}{x dx}$
SERIE
\sum_{dicitura sotto}^{dicitura sopra}{argomento sommatoria}
ESEMPIO
\sum_{i=1}^{n}{5^i}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\sum_{i=1}^{n}{5^n}$
PRODUTTORIE
\prod_{dicitura sotto}^{dicitura sopra}{argomento produttoria}
ESEMPIO
\prod_{i=1}^{n}{6n+2}
Per vedere ciò che produce bisogna mettere prima della formula un dollaro $ e dopo la formula un altro dollaro e diventa:
$\prod_{i=1}^{n}{6n+2}$
FRECCE LATEX
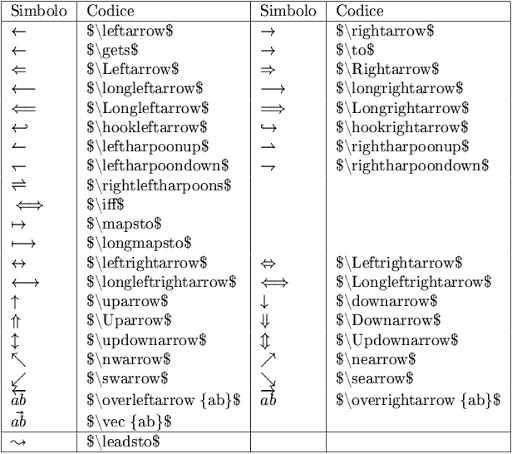
SIMBOLI MATEMATICI LATEX

ACCENTI LATEX
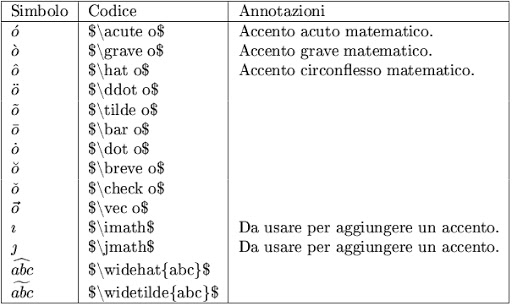
LETTERE GRECHE LATEX
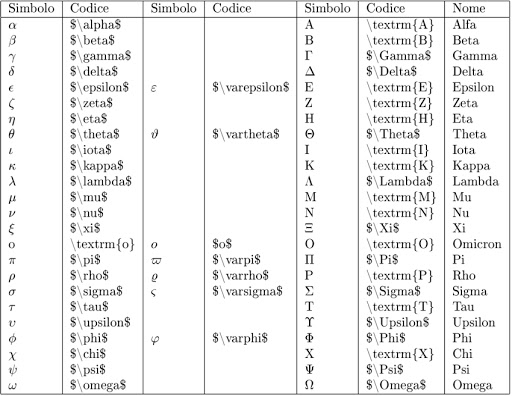
DELIMITATORI
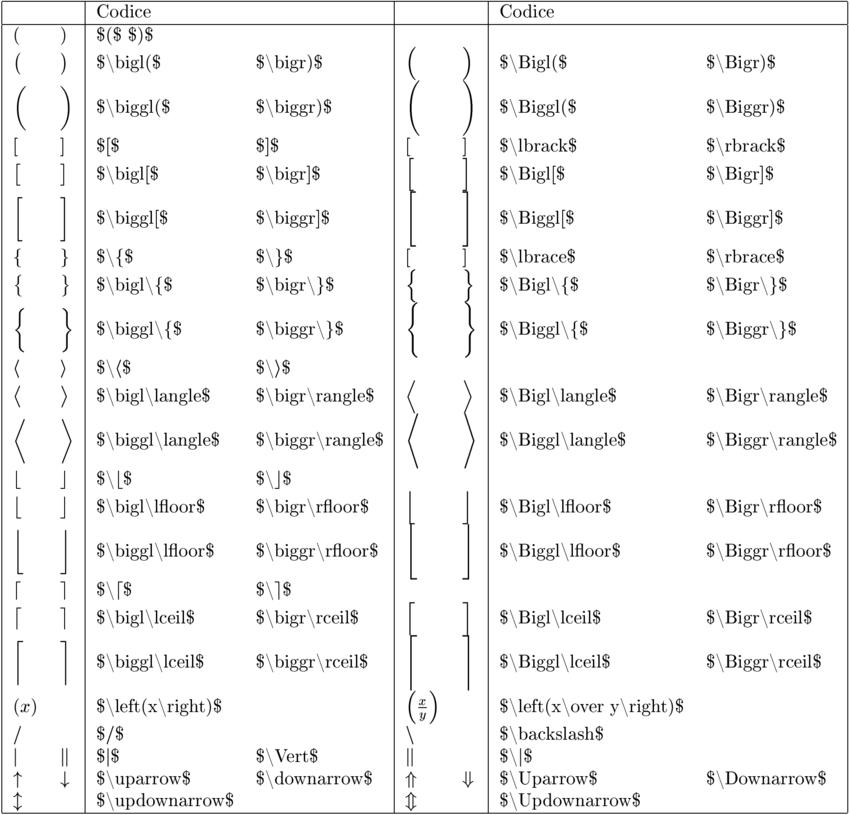
OPERATORI DI RELAZIONE

