I numeri sono alla base della matematica, conoscerli è fondamentale.
Partendo dall’insieme dei numeri naturali , è necessario introdurre l’insieme dei numeri interi Z per poter fare la sottrazione. Introducendo l’insieme dei numeri razionali Q è possibile fare la divisione. Nell’insieme Q è possibile fare le quattro operazioni: addizione, sottrazione, moltiplicazione e divisione.

E’ necessario ampliare Q perché l’estrazione di radice non è interna a tale insieme. A ogni numero razionale corrisponde un numero decimale finito o periodico e viceversa, mentre in alcuni casi l’estrazione di radice ha come risultato numeri decimali illimitati e non periodici.
A ogni punto della retta non corrisponde un numero razionale ma a ogni numero razionale corrisponde un punto sulla retta (corrispondenza biunivoca).
L’insieme dei numeri naturali N è un insieme infinito.
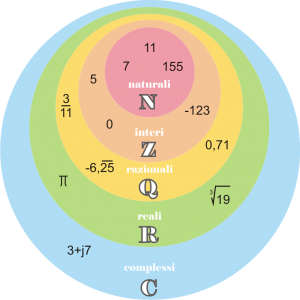
Dal punto di vista insiemistico abbiamo la seguente rappresentazione mediante il diagramma di Eulero-Venn:
DEFINIZIONE
Dato un insieme A, si definisce cardinalità di A il numero degli elementi che appartengono a tale insieme.
La cardinalità può essere finita (insieme finito), o infinita (insieme infinito). L’insieme N costituisce il più piccolo insieme infinito possibile e tutti gli insiemi che hanno la stessa cardinalità di N, si dicono numerabili.
L’insieme Q è denso nell’insieme dei reali R, quindi tra due numeri reali esiste sempre almeno un numero razionale.
R è completo, comprende numeri interi, razionali, irrazionali. In pratica mettendo i punti su una retta, a ogni punto di essa corrisponde un numero reale.
- SOMMA TRA DUE NUMERI REALI
Siano α e β due numeri reali, si ha:
α + β = sup α(n) + β(n)
Dove α(n) e β(n) sono le troncature n-esime di α e β. Ovvero α + β è definito come l’estremo superiore di un insieme che contiene tutte le somme tra tutte le troncature n-esime di α e β. In questo modo è definita la somma tra due numeri reali, come la somma tra due numeri razionali. (Le troncature n-esime, infatti, sono numeri decimali finiti non periodici, e quindi sono razionali).
