Il teorema di Pitagora è uno dei teoremi più noti della geometria euclidea, in particolare riguarda il triangolo rettangolo ed esprime una importante relazione tra i lati: permette di ricavare la misura di uno dei tre lati (uno dei cateti o ipotenusa) conoscendo la misura degli altri due lati.
Enunciato del teorema di Pitagora
Teorema di Pitagora: In ogni triangolo rettangolo, il quadrato costruito sull’ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
Per comprendere meglio in teorema di Pitagora:
- disegniamo un triangolo rettangolo $\mathrm{ABC}$ retto in $\mathrm{A}$;
- indichiamo con $i$ l’ipotenusa (il lato opposto all’angolo retto) e con $c_{1}$ e $c_{2}$ i due cateti;
- costruiamo su ciascun lato un quadrato avente per base quel lato.
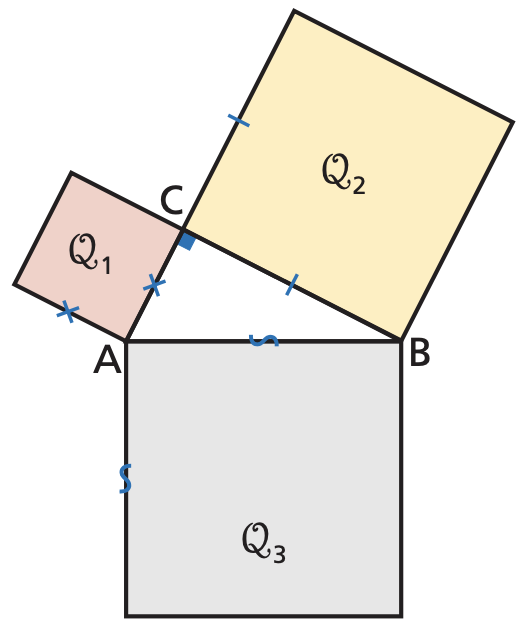
L’area del quadrato $Q_3$ costruito sull’ipotenusa i, è uguale alla somma delle aree dei quadrati $\mathrm{Q}{1}$ e $\mathrm{Q}{2}$ costruiti sui due cateti $c_{1}$ e $c_{2}$. In formule:
$$
\text { Area }{Q_3}=\text { Area }{Q_{1}}+\text { Area }{Q{2}}
$$
Ricordando che l’area del quadrato si ottiene elevando al quadrato la misura del lato, abbiamo:
$A_{Q_{1}}=\text { area del quadrato } Q_{1}=c_{1}^{2}$
$A_{Q_{2}}=\text { area del quadrato } Q_{2}=c_{2}^{2}$
$A_{Q_3}=\text { area del quadrato } Q_3=i^{2}$
Possiamo allora enunciare il teorema di Pitagora ricorrendo alla seguente formula
$$
i^{2}=c_{1}^{2}+c_{2}^{2}
$$
Tale relazione tra i lati ci permette di ricavare le formule inverse del teorema di Pitagora, cioè le formule che esprimono le aree di ciascun quadrato costruito su uno dei due cateti in termini dell’area del quadrato costruito sull’ipotenusa e di quello costruito sull’altro cateto
$c_{1}^{2}=i^{2}-c_{2}^{2}$
$c_{2}^{2}=i^{2}-c_{1}^{2}$
Formule del Teorema di Pitagora
E’ possibile ricavare le formule del teorema di Pitagora direttamente dall’enunciato del teorema, basta considerare le precedenti uguaglianze ed estrarre la radice quadrata. Ottenendo così:
$i=\sqrt{c_{1}^{2}+c_{2}^{2}}$
$c_{1}=\sqrt{i^{2}-c_{2}^{2}}$
$c_{2}=\sqrt{i^{2}-c_{1}^{2}}$
Nella risoluzione dei problemi, se avessimo a che fare con un triangolo rettangolo di cui conosciamo la misura di due lati, potremo calcolare rapidamente la misura del terzo lato.
Dimostrazione del Teorema di Pitagora
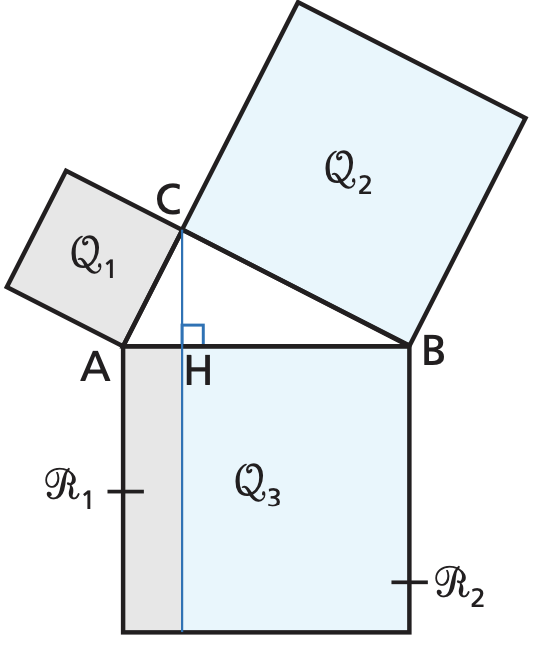
Tracciamo l’altezza $C H$ e prolunghiamola in modo da scomporre il quadrato $Q_{3}$ nei rettangoli $\mathscr{R}{1}$ e $\mathscr{R}{2}$:
$$
Q_{3} \doteq \mathscr{R}{1}+\mathscr{R}{2}
$$
L’altezza $C H$ individua sull’ipotenusa i segmenti $A H$ e $B H$, proiezioni dei cateti. Inoltre $A H$ e $B H$ sono le basi di $\mathscr{R}{1}$ e $\mathscr{R}{2}$, che hanno i lati congruenti alla proiezione di un cateto e all’ipotenusa. Quindi, per il primo teorema di Euclide, abbiamo:
$$
\mathcal{Q}{1} \doteq \mathscr{R}{1}, \quad Q_{2} \doteq \mathscr{R}{2} $$ Poiché somme di figure equivalenti sono equivalenti, risulta: $$ \mathscr{R}{1}+\mathscr{R}{2} \doteq \mathcal{Q}{1}+\mathcal{Q}{2} $$ Essendo $Q{3} \doteq \mathscr{R}{1}+\mathscr{R}{2} \mathrm{e} \mathscr{R}{1}+\mathscr{R}{2} \doteq Q_{1}+Q_{2}$, per la proprietà transiti-
va dell’equivalenza si ottiene:
$$
Q_{3} \doteq Q_{1}+Q_{2} .
$$
Esempio di applicazione del teorema di Pitagora
I cateti di un triangolo rettangolo misurano, rispettivamente, 6 cm e 8 cm. Quanto misura l’ipotenusa?
Questo è uno tra i più classici che riguardano il Teorema di Pitagora: il problema chiede di trovare la misura dell’ipotenusa di un triangolo rettangolo, di cui si conosce la misura dei due cateti.
Per svolgere questo problema è sufficiente applicare la prima delle tre formule sopra riportate:
$i=\sqrt{c_{1}^{2}+c_{2}^{2}}$
Sostituendo i valori, si ottiene:
$i=\sqrt{c_{m}^{2}+c_{M}^{2}}=\sqrt{6^{2}+8^{2}}=\sqrt{36+64}=\sqrt{100}=10 \mathrm{~cm}$
Inverso del teorema di Pitagora
L’inverso del teorema di Pitagora è utile per capire se un qualsiasi triangolo, di cui si conosce o si può ricavare la misura dei lati, è o meno un triangolo rettangolo.
Teorema inverso: Un triangolo nel quale la somma dei quadrati costruiti su due lati è equivalente al quadrato costruito sul terzo lato è rettangolo.
Ovvero se $a$,$b$,$c$ siano i lati se $a^2+b^2=c^2$ allora il triangolo è rettangolo.
