Si definisce pendenza di una retta la tangente dell’angolo $\alpha$ che la retta forma con il piano orizzontale. In pratica esprime l’inclinazione della retta rispetto all’asse delle ascisse.
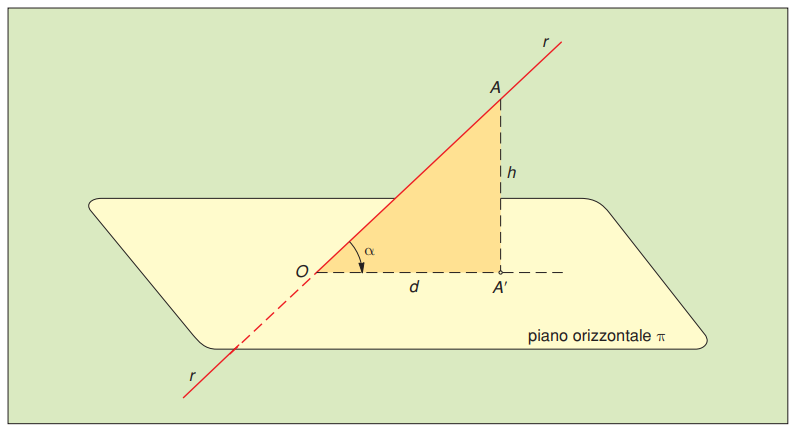
Se consideriamo un punto $A$ sulla retta $r-r$, il punto $A^{\prime}$ rappresenta la sua proiezione sul piano orizzontale $\pi ;$ indicando poi con $O$ il punto di intersezione tra la retta e il piano, si viene a formare il triangolo rettangolo $O A A^{\prime}$ (retto in $A^{\prime}$ ). Esprimendo la definizione di tangente nell’ambito di tale triangolo, e utilizzando le notazioni rappresentate in figura , potremo riscrivere l’espressione precedente nel seguente modo:
$$
p=\frac{h}{d}
$$
La pendenza di una retta, essendo definita dalla tangente di un angolo, è un numero puro; questo viene assunto positivo quando si considera il verso in salita della retta $r-r$, negativo quando si considera il verso in discesa.
Una retta orizzontale ha pendenza nulla perché tg $0^{\mathrm{c}}=0$; una retta inclinata di $50^{\mathrm{c}}$
di una retta prossima alla verticale è infinitamente grande, perché tg $100^{\mathrm{c}}=\infty$.
Nella pratica vengono considerate rette poco inclinate rispetto all’orizzontale, le cui pendenze risultano perciò inferiori all’unità. Pertanto, nel linguaggio pratico, si usa esprimere la pendenza in «per cento», così che, per esempio, una pendenza $p=0,0558$ diventa $p=5,58 \%$.
Formule per calcolare la pendenza di una retta
In base alle informazioni che si hanno a disposizione esistono varie formule che permettono di trovare la pendenza di una retta. Analizziamo di seguito le varie formule:
Pendenza di una retta in forma esplicita
Se la retta è data in forma esplicita ha equazione della forma
$y=m x+q$
ed il coefficiente della $x$ è proprio la pendenza della retta.
Pendenza di una retta in forma implicita
L’equazione di una retta in forma implicita è
$a x+b y+c=0$, con $b \neq 0$
La pendenza in questo caso è l’opposto del rapporto tra il coefficiente della $x$ ed il coefficiente della y, ossia
$$
m=-\frac{a}{b}, \text { con } b \neq 0
$$
Pendenza di una retta note le coordinate di due punti
Se si conoscono le coordinate cartesiane di due punti P e Q appartenenti alla retta
$P\left(x_{P}, y_{P}\right)$ e $Q\left(x_{Q}, y_{Q}\right)$, con $x_{P} \neq y_{Q}$
allora la pendenza della retta si ottiene dal rapporto tra la differenza delle ordinate e la differenza delle ascisse dei due punti:
$$
m=\frac{y_{Q}-y_{P}}{x_{Q}-x_{P}}, \text { con } x_{Q} \neq x_{P}
$$
