Parallelepipedo rettangolo

Un parallelepipedo rettangolo è un tipo specifico di parallelepipedo in cui tutte le facce sono rettangoli, cioè hanno angoli interni di 90 gradi. Ciò significa che le facce opposte sono congruenti e parallele tra loro, e le facce adiacenti sono perpendicolari tra loro.

In un parallelepipedo rettangolo, le tre dimensioni sono lunghezza, larghezza e altezza e ogni coppia di dimensioni adiacenti è perpendicolare tra loro. In particolare, le dimensioni lunghezza e larghezza definiscono la base del parallelepipedo rettangolo, mentre l’altezza è la dimensione che corre perpendicolarmente alla base.

In generale, un parallelepipedo rettangolo è un solido geometrico regolare molto comune, che ha molte applicazioni pratiche in ingegneria, architettura e scienze fisiche, come ad esempio il calcolo del volume di un contenitore rettangolare.

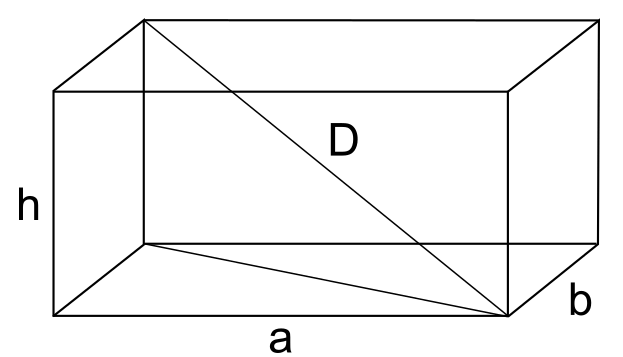
Definizione di parallelepipedo rettangolo
Un parallelepipedo rettangolo è un parallelepipedo retto in cui le basi sono date da due rettangoli.
In modo del tutto equivalente un parallelepipedo rettangolo può essere definito come:

• un prisma retto avente come basi due rettangoli;
• un poliedro che ha come facce 6 rettangoli.
• un esaedro avente come facce dei rettangoli;

Formule del parallelepipedo rettangolo

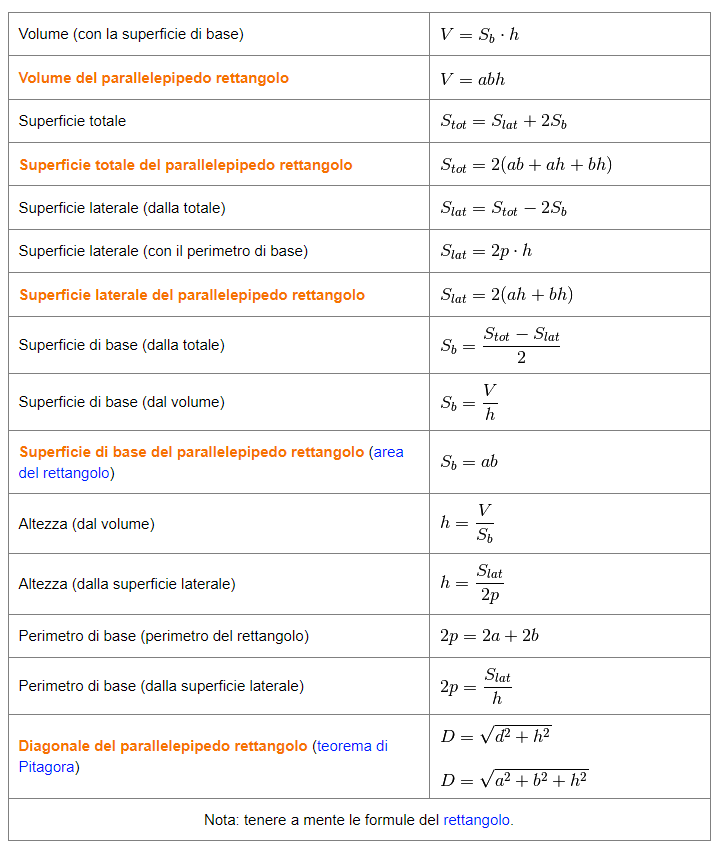
Proprietà del parallelepipedo rettangolo

Il parallelepipedo rettangolo ha molte proprietà interessanti. Ecco alcune delle più importanti:

1. Ha 6 facce, 12 spigoli e 8 vertici.
2. Tutte le facce sono rettangoli e quindi tutti gli angoli interni sono di 90 gradi.
3. Le facce opposte sono parallele e congruenti.
4. Le facce adiacenti sono perpendicolari tra loro.
5. Le diagonali di ogni faccia si intersecano nel centro della faccia stessa.
6. Le diagonali di un parallelepipedo rettangolo sono tutte congruenti tra loro.
7. La somma delle lunghezze dei lati di ogni faccia è uguale alla somma delle lunghezze dei lati delle facce opposte.
8. Il volume del parallelepipedo rettangolo è dato dal prodotto delle sue tre dimensioni: V = lunghezza x larghezza x altezza.
9. L’area totale del parallelepipedo rettangolo è data dalla somma delle aree delle sue sei facce: A = 2(larghezza x altezza) + 2(lunghezza x altezza) + 2(lunghezza x larghezza).

Queste proprietà fanno del parallelepipedo rettangolo un solido geometrico molto utile e versatile, ampiamente utilizzato in molte applicazioni pratiche.