La derivata di una funzione costante
- La derivata di una funzione costante è 0:
$$D k=0$$
Interpretazione grafica
Dal grafico della funzione y = k è intuitivo notare che la tangente al grafico in ogni suo punto è rappresentata da una retta parallela all’asse x, quindi on coefficiente angolare m = f'(x) = 0.

DIMOSTRAZIONE
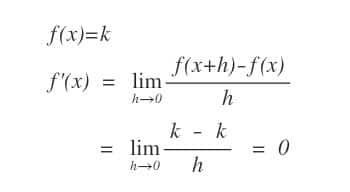
La derivata di una funzione lineare
- La derivata della funzione lineare f (x) = x è f ‘(x) = 1:
$$D x=1$$
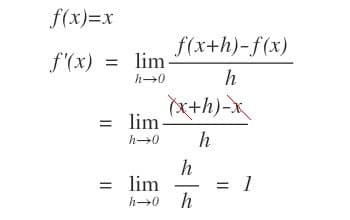
La derivata della potenza $x^n$
- La derivata della variabile x elevata a n è uguale a $n\cdot x^{n-1}$
$$D x^n = n\cdot x^{n-1}$$
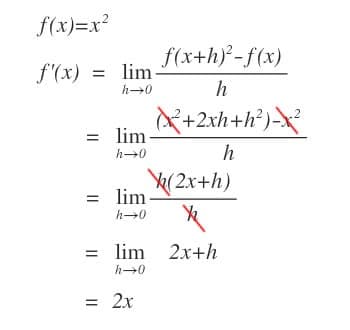
La derivata della radice
- Una radice ennesima della variabile x può essere trasformata in una potenza di x elevata alla frazione $\frac{1}{n}$. In questo modo si può applicare la formula della derivata di una potenza.
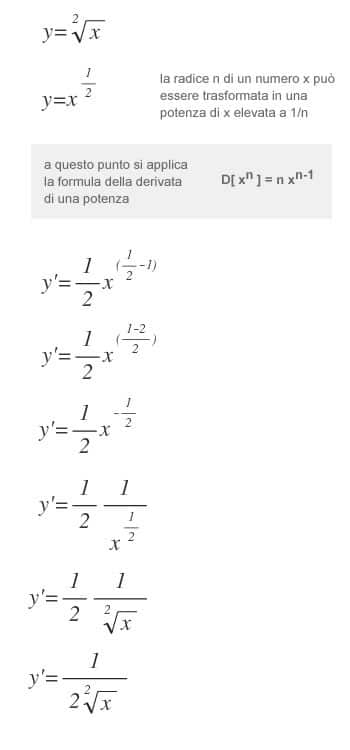
La derivata del reciproco
- La derivata del reciproco può essere dimostrata in modo semplice considerando il reciproco come la potenza di un numero negativo.

La derivata della funzione seno
- La derivata della funzione seno $f(x) = \sin x$, con x espresso in radianti, è $f'(x)=\cos x$.
$$D \sin x = \cos x$$
La derivata della funzione coseno
- La derivata della funzione coseno $f(x) = \cos x$ , con x espresso in radianti, è $f ‘ (x) = – \sin x$.
$$D \cos x = – \sin x$$
La derivata della funzione $a^x$
- La derivata della funzione $f(x)=a^x$ è $f'(x)=a^x \ln a$.
$$D a^x = a^x \ln a$$
In particolare per la funzione esponenziale si ha:
$$D e^x=e^x$$
La derivata della funzione logaritmica
- La derivata della funzione logaritmica $f(x)=\log \underset{a}{} x$ è $f'(x)=\frac{1}{x}\log \underset{a}{} e$
$$D \log \underset{a}{} x=\frac{1}{x}\log \underset{a}{} e$$
In particolare,
$$D \ln x = \frac{1}{x}$$
In sintesi si ha:

INDICE
