La distanza di un punto da una retta, o distanza punto-retta fa riferimento a una formula che permette di calcolare la distanza di un punto da una retta partendo dalle coordinate del punto e dall’equazione della retta.
Dati un punto $P$ ed una retta $r$ nel piano cartesiano, si definisce la distanza punto retta $d(P, r)$ come la minima distanza tra il punto $P$ e tutti i punti che giacciono sulla retta.
$$
d(P, r)=\min {d(P, Q) \text { tale che } Q \in r}
$$
Si può anche definire la distanza di un punto da una retta come la distanza tra il punto $P$ dalla sua proiezione ortogonale sulla retta $r$, cioè la lunghezza del segmento $P P^{\prime}$ che congiunge il punto $P$ perpendicolarmente alla retta.
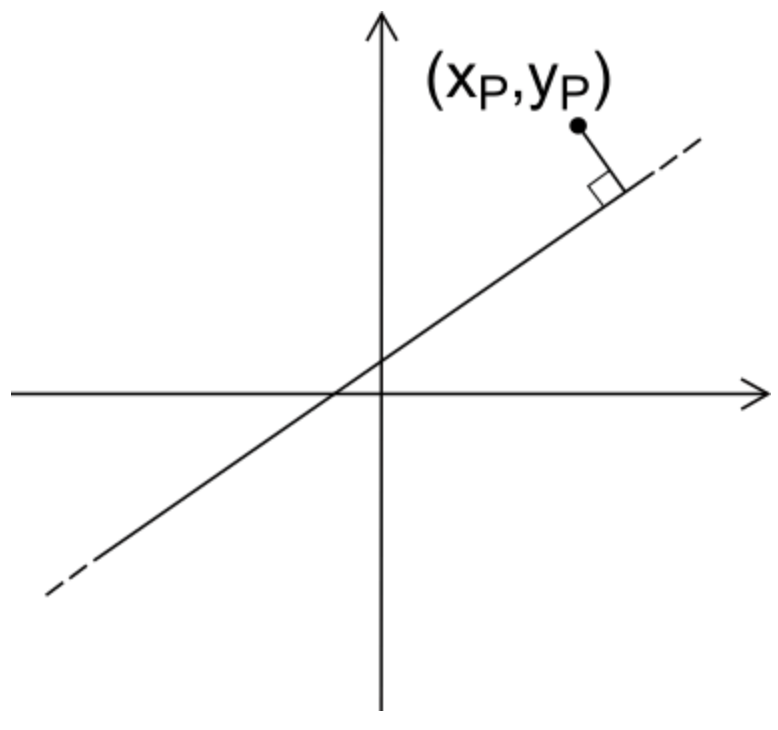
Se il punto appartiene alla retta, la distanza $d(P, r)$ è per definizione nulla, vale a dire: $d(P, r)=0$.
Formule della distanza punto retta
Sia $P$ il punto, indichiamone le coordinate cartesiane con $\left(x_{P}, y_{P}\right)$ e sia $r$ la retta.
A seconda che l’equazione della retta $r$ sia data in forma implicita
$$
a x+b y+c=0
$$
o in forma esplicita
$$
y=m x+q
$$
possiamo ricorrere a due formule del tutto equivalenti.
Distanza di un punto da una retta data in forma implicita
$$d(P, r)=\frac{\left|a x_{P}+b y_{P}+c\right|}{\sqrt{a^{2}+b^{2}}}$$
Al numeratore abbiamo la valutazione del primo membro dell’equazione della retta in forma implicita nelle coordinate del punto, il tutto in valore assoluto. Al denominatore la radice quadrata della somma dei quadrati dei coefficienti associati ai termini di grado 1 nell’equazione della retta.
Distanza di un punto da una retta data in forma esplicita
$$d(P, r)=\frac{\left|y_{P}-\left(m x_{P}+q\right)\right|}{\sqrt{1+m^{2}}}$$
In questo caso si riscrive l’equazione in forma esplicita portando tutto al primo membro, si valuta nelle coordinate del punto e se ne considera il modulo; fatto ciò, si divide il tutto per la radice quadrata della somma dei quadrati dei coefficienti dei termini di grado 1 nell’equazione della retta.
Come passare dalla forma esplicita alla forma implicita?
Abbiamo due opzioni: o memorizziamo la formula vista nei paragrafi precedenti e trasformiamo l’equazione della retta da implicita a esplicita, oppure memorizziamo la formula con la retta espressa in forma implicita. Tale formula è:
$$
d(P, r)=\frac{\left|a x_{P}+b y_{p}+c\right|}{\sqrt{a^{2}+b^{2}}}
$$
è possibile facilmente passare da una forma all’altre considerando che $\mathrm{m}=-\mathrm{a} / \mathrm{b}$ e $\mathrm{q}=-\mathrm{c} / \mathrm{b}$.
$$
d(P, r)=\frac{\left|y_{p}-\left(m x_{P}+q\right)\right|}{\sqrt{m^{2}+1}}=\frac{\left|y_{p}-\left(-\frac{a}{b} x_{P}-\frac{c}{b}\right)\right|}{\sqrt{\left(-\frac{a}{b}\right)^{2}+1}}
$$
moltiplicando numeratore e denominatore per b:
$$
d(P, r)=\frac{b\left|y_{p}-\left(-\frac{a}{b} x_{P}-\frac{c}{b}\right)\right|}{b \sqrt{\left(-\frac{a}{b}\right)^{2}+1}}=\frac{\left|b y_{p}+a x_{P}+c\right|}{\sqrt{a^{2}+b^{2}}}
$$
Esempio di calcolo della distanza di un punto da una retta
Calcoliamo la distanza del punto $P \equiv(-2,1)$ dalla retta $r$ di equazione $3 x+4 y-3=0$.
Cominciamo con l’identificare i coefficienti: $a=3, b=4, c=-7$
Le coordinate del punto sono $x_{P}=-2$ e $y_{P}=1$
Quindi sostituendo abbiamo
$$
\operatorname{dist}(P, r)=\frac{|3 \cdot(-2)+4 \cdot 1-3|}{\sqrt{3^{2}+4^{2}}}=\frac{|-5|}{\sqrt{25}}=\frac{5}{5}=1
$$
Questo esempio mostra come il valore assoluto sia indispensabile per evitare che il risultato sia negativo: una distanza infatti può essere soltanto positiva.
