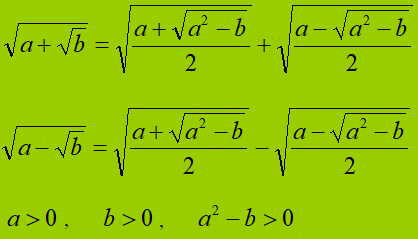
Le condizioni di esistenza
Le condizioni di esistenza dei radicali sono comunemente chiamate Dominio e sono di estrema importanza nello studio di una funzione.
Per determinarlo bisogna porre la condizione che essa sia maggiore o uguale a 0, indipendentemente dall’indice di radice.
ESEMPIO
$\sqrt[3]{x-1}$ ha come condizione di esistenza $x-1\geq 0$ ossia C.E: $x \geq 1$.
TEOREMA
Dato un radicale, si può ottenere un radicale equivalente moltiplicando per uno stesso numero naturale (diverso da 0) sia l’indice del radicale sia l’esponente del radicando.
Questa rappresenta la proprietà invariantiva dei radicali.
ESEMPIO
$$\sqrt[2]{2} =\sqrt[2\cdot 3]{2^3}=\sqrt[6]{8}$$
La semplificazione dei radicali
Dato un radicale, si può ottenere un radicale equivalente dividendo l’indice della radice e l’esponente del radicando per un divisore comune.
ESEMPIO
$$\sqrt[9]{5^6} =\sqrt[9: 3]{5^{6:3} }=\sqrt[3]{5^2} $$
DEFINIZIONE
Un radicale si dice irriducibile, cioè non semplificabile, quando il suo indice e l’esponente del radicando sono primi fra loro.
OSSERVAZIONE
Per semplificare un radicale e renderlo irriducibile, occorre:
- cercare il M.C.D. fra indice ed esponente del radicando;
- dividere l’indice e l’esponente per il loro M.C.D.
ESEMPIO
Rendiamo irriducibile il radicale $\sqrt[20]{7^{12} } $
- M.C.D. (20;12) = 4
- dividiamo per 4 l’indice e l’esponente del radicando: $\sqrt[20]{7^{12} }$=$ \sqrt[20:4]{7^{12:4} } =\sqrt[5]{7^3} $
La semplificazione e il valore assoluto
Se bisogna studiare il valore di un radicando negativo con esponente pari bisogna porre all’interno il valore assoluto.
In generale, se n è pari:
$$\sqrt[n]{a^{n} } =|a|$$
che nel caso di n=2 diventa:
$$\sqrt[2]{a^{2} } =|a|$$
La riduzione di radicali allo stesso indice
Applicando la proprietà invariantiva, si possono trasformare due o più radicali in altri che hanno lo stesso indice.
Bisogna fare i seguenti passaggi:
- cercare il m.c.m. fra gli indici;
- trasformare ogni radicale in uno equivalente, che ha per indice il m.c.m. trovato.
ESEMPIO
Riduciamo al minimo comune indice i seguenti radicali.
$\sqrt[5]{2a^{2} }$ e $\sqrt[4]{a^{3} }$ con a positiva.
- m.c.m. (5;4) = 20
- eleviamo ogni radicando al quoziente fra il m.c.m. e l’indice, rispettivamente 20 : 5 = 4 e 20 : 4 = 5
$$\sqrt[5]{2a^{2} }=\sqrt[5\cdot 4]{(2a^2)^4}=\sqrt[20]{16a^8} $$
$$\sqrt[4]{a^{3} }=\sqrt[4\cdot 5]{(a^3)^5}=\sqrt[20]{a^{15}} $$.
La moltiplicazione fra radicali
Il prodotto di due radicali con lo stesso indice è un radicale che ha per indice lo stesso indice e per radicando il prodotto dei radicandi, ossia
$$\sqrt[n]{a} \cdot \sqrt[n]{b} =\sqrt[n]{a\cdot b} $$
con a e b reali, $a\geq 0, b\geq 0$ e n naturale, $n\neq 0$.
OSSERVAZIONE
Se i radicali hanno indice diverso, per moltiplicarli è necessario ridurli al loro minimo comune indice,
La divisione fra radicali
Il quoziente di due radicali, il secondo diverso da zero, con lo stesso indice è un radicale che ha per indice lo stesso indice e per radicando il quoziente dei radicandi, ossia
$$\sqrt[n]{a} : \sqrt[n]{b} =\sqrt[n]{a : b} $$
Il trasporto di un fattore fuori dal segno di radice
Tramite la seguente proprietà è possibile trasportare fuori dal segno di radice i fattori del radicando che hanno come esponente un multiplo di n.
Considerato il radicale $\sqrt[n]{a^m}$ con $a\geq 0, m\geq n$ e indicati con q il quoziente di m : n e con r il resto ($m= n\cdot q + r$) si ha:
$$\sqrt[n]{a^m} =\sqrt[n]{a^{n\cdot q}\cdot a^r } =\sqrt[n]{a^{n\cdot q} } \cdot \sqrt[n]{a^{r} } =a^q\sqrt[n]{a^r}$$
Quando si vuol portare fuori radice un fattore di cui non si conosce il segno, si scrive tale fattore in valore assoluto.
La potenza di un radicale
La potenza m-esima di un radicale è un radicale che ha per indice lo stesso indice e per radicando la potenza m-esima del radicando, ossia
$$(\sqrt[n]{a} )^m=\sqrt[n]{a^m} $$
con n e m naturali, $n\neq 0 e m\neq 0$ e a reale $a\geq 0$.
OSSERVAZIONE
$$(\sqrt[n]{a} )^n=a$$.
La radice di un radicale
La potenza m-esima di un radicale di indice n è un radicale che ha per indice il prodotto degli indici $m\cdot n$ e per radicando lo stesso radicando.
$$\sqrt[m]{\sqrt[n]{a} } =\sqrt[m\cdot n]{a} $$
con n e m naturali, $n\neq 0 e m\neq 0$ e a reale $a\geq 0$.
Radicali simili
Due radicali irriducibili si dicono simili quando hanno lo stesso indice, lo stesso radicando e possono essere diversi solo per il fattore che li moltiplica, detto coefficiente del radicale.
OSSERVAZIONE
A volte due radicali possono essere trasformati in radicali simili portando fuori dalla radice alcuni fattori.
La somma algebrica di radicali simili
La somma algebrica di due o più radicali simili è il radicale, simile ai dati, che ha come coefficiente la somma algebrica dei coefficienti.
ESEMPIO
$$a\sqrt{2} +\sqrt{2}=(a+1)\sqrt{2} $$
La razionalizzazione del denominatore di una frazione
Razionalizzare il denominatore di una funzione significa trasformare la frazione in una equivalente che non ha radicali a denominatore.
Per razionalizzare il denominatore di una frazione si applica la proprietà invariantiva delle frazioni, moltiplicando numeratore e denominatore per uno stesso fattore diverso da zero.
Esaminiamo i casi più comuni.
CASO 1: Il denominatore è un unico radicale
Se il denominatore contiene un radicale quadratico, basta moltiplicare numeratore e denominatore per il radicale stesso.
ESEMPIO
$$\frac{6}{\sqrt{2} } =\frac{6}{\sqrt{2} } \cdot \frac{\sqrt{2} }{\sqrt{2} } =\frac{6\cdot \sqrt{2} }{\sqrt{2} } =3\cdot \sqrt{2} $$
Il risultato ottenuto non contiene radicali al denominatore.
CASO 2: Il denominatore è la somma o la differenza di due termini, dei quali almeno uno è un radicale quadratico
ESEMPIO
$$\frac{8}{\sqrt{7} +\sqrt{2} } \cdot \frac{(\sqrt{7}-\sqrt{2} )}{\sqrt{7}-\sqrt{2} } =\frac{8(\sqrt{7}-\sqrt{2} )}{(\sqrt{7} )^2-(\sqrt{2} )^2} =\frac{8(\sqrt{7 } -\sqrt{2} )}{5} $$
I radicali quadratici doppi
Si chiama radicale quadratico doppio un’espressione del tipo:
$\sqrt{a+\sqrt{b} }$ oppure $\sqrt{a-\sqrt{b} }$
Un radicale doppio può essere trasformato nella somma o nella differenza di due radicali semplici solo quando l’espressione $a^2-b$ è il quadrato di un numero razionale o di un’espressione che non contiene radicali.
Valgono le due uguaglianze: