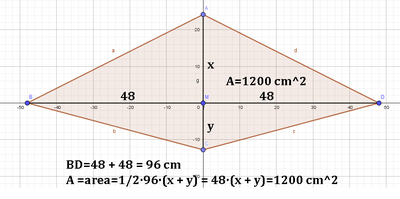
Buona giornata a tutti; vado a postare un problema geometrico che mi sta creando delle difficoltà per giungere alla sua soluzione; ecco il testo : nel quadrilatero ABCD le diagonali sono perpendicolari e si ha BM = MD = 48 cm. Si conosce l'area del quadrilatero che è di cm^ 1200 e che il lato maggiore supera di cm. 8 la sua proiezione ortogonale sulla diagonale AC. Determinare il perimetro del quadrilatero. Risposta cm. 140. Chiedo per favore lo svolgimento passaggio per passaggio e se possibile il disegno del quadrilatero. Ringrazio anticipatamente coloro che vorranno, ancora una volta, aiutarmi.