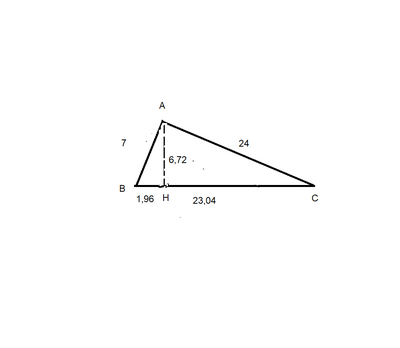
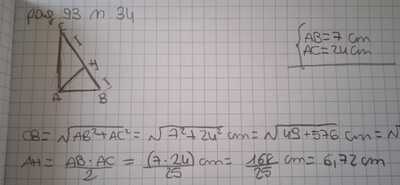I cateti di un triangolo rettangolo misurano $7 \mathrm{~cm}$ e $24 \mathrm{~cm} .$ Calcola:
a. I'altezza relativa all'ipotenusa
b. le misure dei segmenti in cuil'ipotenusa è divisa dall'altezza a essa relativa $[6,72 \mathrm{~cm} ;$
$23,04 \mathrm{~cm}]$
come fare la lettera b