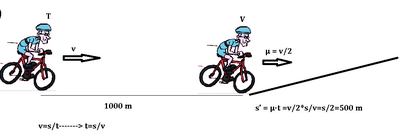
Un ciclista $T$ segue un ciclista $V$ a una distanza di $1 km$ e i due procedono alla medesima velocità. La strada improvvisamente inizia a salire con pendenza costante. Ammesso che ciascuno dei ciclisti dimezzi la propria velocità nell'istante in cui inizia la salita, qual è la loro distanza quando ambedue sono nel tratto in salita?
A $1 km$
B $2 km$
C $500 m$
D $250 m$
E Non è determinabile se non si conosce la velocità iniziale dei ciclisti
Quando i due ciclisti si trovano in piano sono separati da una distanza temporale pari a $t=\frac{1000 m}{v}$ dove $v$ è la velocità comune dei due ciclisti quando si trovano sul piano. Quando entrambi i ciclisti sono nel tratto in salita, la loro distanza spaziale è diminuita, la loro velocità è dimezzata, ma la distanza temporale è rimasta la stessa. Indicando con $x$ la distanza spaziale dei due corridori che si trovano in salita si ha:
$$
t=\frac{1000 m }{v}=\frac{x}{v / 2} \Rightarrow x=500 m \text { (risposta C) }
$$
Salve, ipotizzando che all'inizio della salita il ciclista V (quello che precede T) mantenga la precedente velocità costante, invece il ciclista T la dimezzi, come cambia la risoluzione?