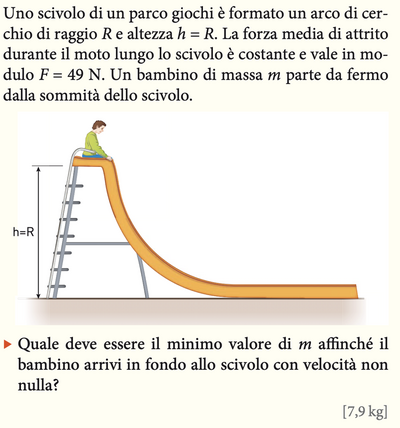
Scendendo dallo scivolo, il bambino percorre una distanza pari a un quarto di una circonferenza di raggio $\mathrm{R}$, ovvero:
$$
\Delta x=\frac{1}{4} 2 \pi R=\frac{\pi R}{2}
$$
Esprimo il lavoro compiuto dalla forza d'attrito in funzione dello spostamento applicando la definizione:
$$
L_{a t t}=F \Delta x \cos \left(180^{\circ}\right)=-F \frac{\pi R}{2}
$$
Esprimo ora la stessa grandezza in funzione della variazione dell'energia meccanica, imponendo che il bambini arrivi in fondo allo scivolo con velocità nulla (in questo modo trovo il valore minimo della massa richiesto dal quesito):
$$
L_{a t t}=\Delta E_m=K_f-U_0=-U_0=-m g h=-m g R
$$
Eguagliando le due relazioni ottengo:
$$
\begin{gathered}
-F \frac{\pi R}{2}=-m g R, \text { da cui ricavo che: } \\
m=\frac{F \pi}{2 g}=\frac{49 N \times \pi}{2 \times 9,8 \frac{m}{s^2}}=7,9 \mathrm{~kg}
\end{gathered}
$$