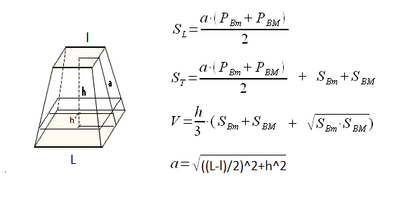
IN UN TRONCO DI PIRAMIDE A BASI PARALLELE HA L AREA DELLE BASI 27 E 147 È l altezza luna12 cm
A che distanza bisogna condurre un piano paralleli lo alle basi in modo che i volumi dei due tronchi ottenuti sia nel rapporto 189/127
SAPENDO che il tronco maggiore è quello che ha una base la base minore del tronco dato?