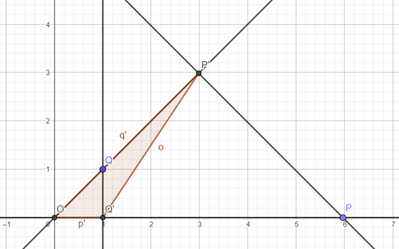
Due semirette $a$ e $b$, di origine $O$, formano un angolo acuto $\alpha$ tale che $\sin \alpha=\frac{1}{3}$. Sia $P$ il punto appartenente alla semiretta $a$ tale che $\overline{O P}=6 m$ e $Q$ il punto appartenente alla semiretta $b$ tale che $\overline{O Q}=m$. Indicate con $P^{\prime}, Q^{\prime}$, rispettivamente, la proiezione di $P$ su $b$ e la proiezione di $Q$ su $a$, calcola l'area del triangolo $P^{\prime} O Q^{\prime}$.
$$
\left[\frac{8}{9} m^2\right]
$$
1
punto
Livello 0
Essendo OQQ' triangolo rettangolo in Q' abbiamo che:
$OQ' = OQ cos\alpha = OQ \sqrt{1-sin^2\alpha} = m \sqrt{1*(1/3)^2} = \frac{2\sqrt{2}}{3} m$
Analogamente OPP' è retto in P':
$OP' = OP \cos\alpha = OP\sqrt{1-sin^2\alpha} = 6m\sqrt{1*(1/3)^2} = 4\sqrt{2} m$
Allora l'area di OP'Q' è:
$ A= \frac{1}{2} OQ'*OP' sin\alpha = \frac{1}{2}* \frac{2\sqrt{2}}{3} m * 4\sqrt{2} m * \frac{1}{3} = \frac{8}{9} m^2$
Noemi
9874
punti
Livello 5
@n_f 👍👍👍
