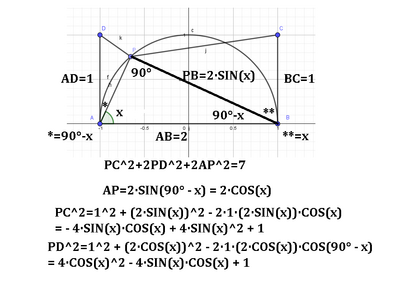
Presi i punti $D$ e $C$ rispettivamente sulle tangenti in $A$ e $B$ a una semicirconferenza di diametro $\overline{A B}=2$, si abbia $\overline{A D}=\overline{C B}=1$. Sia $P$ un punto sulla semicirconferenza. Posto $\overrightarrow{P A B}=x$, risolvi l'equazione: $\overline{P C}^2+2 \overline{P D}^2+2 \overline{A P}^2=7$.N251
9
punti
Livello 0
Ho completato il mio post che era rimasto in sospeso. Buona Domenica.
Con riferimento alla figura allegata puoi scrivere:
- 4·SIN(x)·COS(x) + 4·SIN(x)^2 + 1
2·(4·COS(x)^2 - 4·SIN(x)·COS(x) + 1)
2·(2·COS(x))^2
------------------------------------------(SOMMA)
12·COS(x)^2 - 12·SIN(x)·COS(x) + 7
Ottieni quindi l'equazione:
12·COS(x)^2 - 12·SIN(x)·COS(x) = 0
12·COS(x)·(COS(x) - SIN(x)) = 0
che fornisce soluzione:
x = pi/4 ∨ x = pi/2
94792
punti
Genius II
