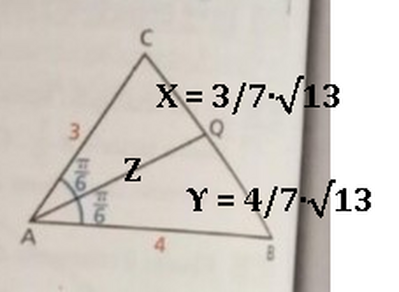
Osserva il triangolo della figura.
a. Calcola le misure di $B C, C Q$ e $B Q$.
b. Determina $\cos A \hat{B} C$ e la lunghezza di $A Q$.
c. Indicato con $P$ un punto della bisettrice $A Q$ e con $x$ la misura del segmento $A P$, determina la funzione
$$
f(x)=\overline{A P^2}+\overline{B P^2}+\overline{C P^2}
$$
eil valore minimo assunto da essa nei limiti imposti dal problema.
106
punti
Livello 0
Ho svolto per il momento pure il secondo punto. Buona notte.
Svolgo il primo punto. Dopo cena (se mi ricorderò) svolgerò gli altri.
Th di Carnot
Con le solite convenzioni per i triangoli scrivo:
a = √(b^2 + c^2 - 2·b·c·COS(pi/3))
a = √(3^2 + 4^2 - 2·3·4·COS(pi/3))
a = √13
{b/c = 3/4 = Χ/Υ (teorema bisettrice)
{X + Y = √13
Avendo posto: CQ = X ; BQ = Y
3/4----> 3 + 4 = 7
Χ = 3/7·√13
Υ = 4/7·√13
Secondo punto
Χ = 3/7·√13 ; Υ = 4/7·√13
Determino il coseno:
3^2 = 4^2 + √13^2 - 2·4·√13·COS(β)
9 = 29 - 8·√13·COS(β)----> COS(β) = (29 - 9)/(8·√13)
quindi: COS(β) = 5·√13/26
ΑQ = Z (vedi figura sopra)
Z = √(4^2 + (4/7·√13)^2 - 2·4·(4/7·√13)·(5·√13/26))
sviluppo i calcoli ed ottengo:
Z = 12·√3/7
Per gli altri due punti è richiesto un bel po' di tempo.
Se mi è possibile riprenderò domani. Ciao.
94774
punti
Genius II
@lucianop il punto 1 già era svolto in altri post, se possibile mi servono gli altri punti
