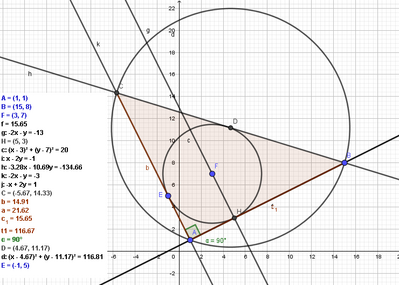
Del triangolo ABC sono noti i vertici A(1;1) e B(15;8)e l'incentro F (3;7). Determina le coordinate del punto C (suggerimento : l'incentro é equidistante dai lati del triangolo). Verifica poi che il triangolo è rettangolo e trova il circocentro.
Risposte : C(-17/3: 43/3) D(14/3; 67/6).
P.S. La soluzione che ho prospettato è la seguente: 1) Distanza tra F e la retta AB di cui si conosce già l'equazione, applicando la formula di una retta passante per 2 punti: la retta ha equazione - x + 2y -1 e la sua distanza dal punto F é 2 radical 5.
2) Impostare il fascio di rette passante per A
3) Impostare il fascio di rette passante per B
4) Imporre che le rette di ciascun fascio abbiano distanza da F uguale a quella già trovata, cioè 2 radical 5
5) Trovare le 2 equazioni delle rette AC e CB, metterle a sistema e ricavare le coordinate di C.
Le possibilità sono 2 : o è sbagliato questo ragionamento, oppure sbaglio dei calcoli.
Per favore, se potete e volete, datemi un aiuto. Grazie molte.