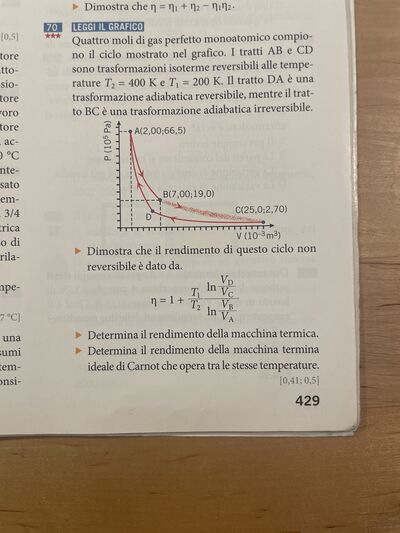
Calcoliamo il lavoro e il calore scambiato per ogni trasformazione.
Nel tratto AB abbiamo un'isoterma per cui:
$ Q_{AB} = L_{AB} = nRT_2 ln \frac{V_B}{V_A}$
Nel tratto BC c'è una adiabatica:
$ Q_{BC} = 0$
$ L_{BC} = -\Delta U = -\frac{3}{2} nR \Delta T = -\frac{3}{2} nR (T_C-T_B)$
Nel tratto CD abbiamo un'altra isoterma:
$ Q_{CD} = L_{CD} = nRT_1 ln \frac{V_D}{V_C}$
Infine nel tratto DA di nuovo adiabatica:
$ Q_{DA} = 0$
$ L_{DA} = -\frac{3}{2} nR (T_A-T_D)$
Il calore totale assorbito è solo quello nel tratto AB, in cui il calore è positivo (in CD invece è negativo):
$ Q_{ass} = Q_{AB} = nRT_2 ln \frac{V_B}{V_A}$
mentre il lavoro totale compiuto è:
$ L = nRT_2 ln \frac{V_B}{V_A} -\frac{3}{2} nR (T_C-T_B) -\frac{3}{2} nR (T_A-T_D)+nRT_1 ln \frac{V_D}{V_C}$
Notiamo però che $T_C = T_D$ e che $T_B=T_A$ essendo CD e AB isoterme, per cui possiamo scrivere:
$ L = nRT_2 ln \frac{V_B}{V_A} -\frac{3}{2} nR (T_D-T_A) -\frac{3}{2} nR (T_A-T_D)+nRT_1 ln \frac{V_D}{V_C}$
e notiamo che i due termini relativi alle adiabatiche si semplificano per cui rimane:
$ L = nRT_2 ln \frac{V_B}{V_A} +nRT_1 ln \frac{V_D}{V_C}$
Dunque il rendimento è:
$ \eta = \frac{L}{Q_{ass}} = \frac{nRT_2 ln \frac{V_B}{V_A} +nRT_1 ln \frac{V_D}{V_C}}{nRT_2 ln \frac{V_B}{V_A}}$
possiamo mettere in evidenza e semplificare nR:
$ \eta = \frac{T_2 ln \frac{V_B}{V_A} +T_1 ln \frac{V_D}{V_C}}{T_2 ln \frac{V_B}{V_A}}$
inoltre possiamo separare la frazione come:
$ \eta = \frac{T_2 ln \frac{V_B}{V_A}}{T_2 ln \frac{V_B}{V_A}} + \frac{T_1 ln \frac{V_D}{V_C}}{T_2 ln \frac{V_B}{V_A}}$
che semplificando è:
$ \eta = 1+\frac{T_1 ln \frac{V_D}{V_C}}{T_2 ln \frac{V_B}{V_A}}$