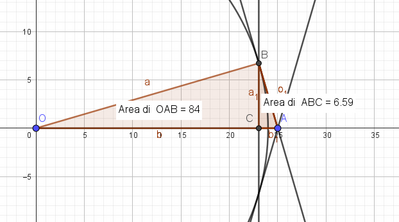
Mi potete spiegare come si risolve questo problema?
Data una circonferenza di centro O e raggio r, scegli un punto A distante dal centro i 25/24 del raggio. Traccia da A una tangente alla circonferenza e chiama B il punto di tangenza; traccia da B la perpendicolare BC ad AO. Calcola il rapporto fra l'area del triangolo AOB e quella del triangolo ACB.
Risultato: 625/49
9
punti
Livello 0
ΑΒ = √(25^2 - 24^2) = misura segmento tangente
ΑΒ = 7 cm (supponiamo tutte le misure in cm!)
ΟC = ΟΒ^2/(ΟΑ) (1° teorema di Euclide)
ΟC = 576/25 cm (=23.04 cm)
ΒC = √(24^2 - (576/25)^2) = altezza triangolo rettangolo OAB relativa all'ipotenusa OA
ΒC = 168/25 cm ( =6.72 cm)
Α(OAB) = 1/2·24·7=84 cm^2
ΑC = 25 - 576/25 = 49/25 cm (=1.96 cm)
Α(ABC) = 1/2·(49/25)·(168/25)= 4116/625 cm^2
Α(OAB)/Α(ABC)=84/(4116/625) = 625/49
94739
punti
Genius II
Ciao non sapevo che la soluzione di questo esercizio fosse già stata richiesta da un altro utente. Comunque ho compreso la tua soluzione e anche il disegno; ti ringrazio e auguro buon pomeriggio.
Buon pomeriggio pure a te.
