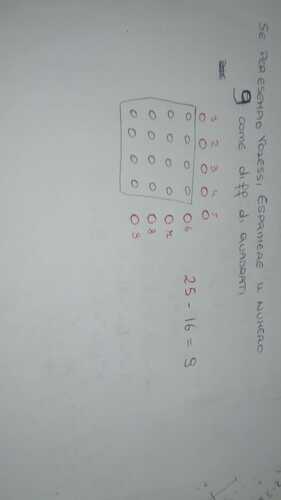
Qualcuno può risolverlo con un ragionamento adatto per studente di seconda media?
Osservando la successione dei numeri quadrati, i Pitagorici scoprirono alcune importanti relazioni relative ai numeri naturali.
Quali tra le seguenti affermazioni è vera?
a) Ogni numero pari può essere scritto come differenza di due numeri quadrati.
b) Ogni numero dispari può essere scritto come differenza di due numeri quadrati.
11945
punti
Livello 7
Ogni numero dispari è effettivamente esprimibile come la differenza di due quadrati consecutivi. Questa dimostrazione non mi sembra idonea però a uno studente di seconda media, che non ha le nozioni algebriche necessarie. L'unica via rimane quella di fare osservare empiricamente che ciò avviene scegliendo due quadrati qualsiasi. Quello che fa in pratica coi disegni è proprio "TOGLIERE" da un quadrato un altro quadrato facendo osservare che la parte evidenziata in verde è composta da un numero dispari di elementi
3817
punti
Livello 4
@anguus90 grazie! Hai confermato quello che pensavo...
@anguus90 @Cenerentola : io sottolinerei anche il fatto che (sempre riferendomi alla figura) quello che rimane sottraendo un quadrato da un altro quadrato è un numero dispari perchè sempre somma di una riga di $n$ cerchietti e di una colonna data da $n-1$ cerchietti, ovvero sempre da una somma di un numero pari e di un numero dispari, che fa sempre dispari.
@anguus90 @Sebastiano Grazie!!!
La differenza d fra due quadrati qualsiasi è il prodotto fra somma e differenza delle basi
* d = a^2 - b^2 = (a + b)*(a - b)
---------------
Se le due basi sono interi consecutivi
* d = a^2 - (a - 1)^2 = (a + (a - 1))*(a - (a - 1)) = (2*a - 1)*(1) = 2*a - 1
che è dispari in quanto predecessore di un doppio.
QUESTO DICE CHE L'AFFERMAZIONE b E' VERA.
---------------
Se le due basi non sono interi consecutivi occorre esaminare i quattro casi delle loro parità.
* dispari/dispari: (a = 2*h + 1) & (b = 2*k + 1) → d = 4*(h^2 + h - k^2 - k) [PARI]
* dispari/pari: (a = 2*h + 1) & (b = 2*k) → d = 4*(h^2 + h - k^2) + 1 [DISPARI]
* pari/dispari: (a = 2*h) & (b = 2*k + 1) → d = 4*(h^2 - k^2 - k) - 1 [DISPARI]
* pari/pari: (a = 2*h) & (b = 2*k) → d = 4*(h^2 - k^2) [PARI]
Questo dice che l'affermazione a e' vera solo per i pari quadrupli, ma che in generale è falsa.
Vedi al link
http://giuseppemerlino.wordpress.com/2011/10/10/espressione-di-un-intero-come-differenza-di-2-quadrati-esatti/
51564
punti
Genius I
@exprof grazie!
naturalmente la B
2^2-1^2 = 3 (dispari)
3^2-2^2 = 9-4 = 5 (dispari)
4^2-3^2 = 16-9 = 7 (dispari)
...e così via
96603
punti
Genius II
