Il polinomio $P(x)=a x^2+b x+c$ è tale che $P(1)=P\left(-\frac{7}{2}\right)=1$ e $P(-5)=19$. Determina il polinomio.
$$
\left[2 x^2+5 x-6\right]
$$
Buonasera, sto cercando di risolvere questo esercizio, più che altro non riesco a capire come impostare il sistema
42
punti
Livello 0
Avrai sbagliato qualche calcolo.
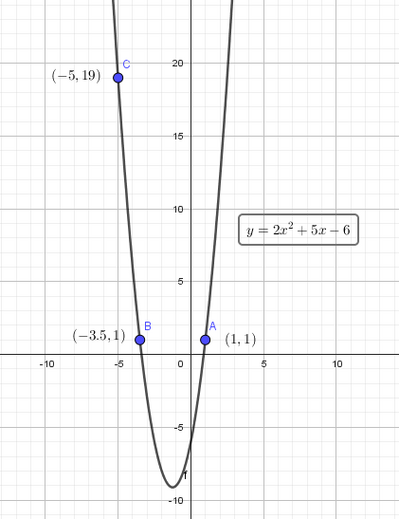
y = a·x^2 + b·x + c parabola ad asse verticale:
{1 = a·1^2 + b·1 + c passa per [1,1]
{1 = a·(- 7/2)^2 + b·(- 7/2) + c passa per [-7/2,1]
{19 = a·(-5)^2 + b·(-5) + c passa per [-5,19]
Quindi:
{a + b + c = 1
{49·a/4 - 7·b/2 + c = 1
{25·a - 5·b + c = 19
Se lo risolvi ottieni: [a = 2 ∧ b = 5 ∧ c = -6]
Risolviamo per sostituzione:
c = -a - b + 1
Quindi
{49·a/4 - 7·b/2 + (-a - b + 1) = 1
{25·a - 5·b + (-a - b + 1) = 19
Quindi
{45·a/4 - 9·b/2 = 0
{24·a - 6·b = 18
---------------------------
{45·a - 18·b = 0
{4·a - b = 3
a = 2·b/5
4·(2·b/5) - b = 3---> 3·b/5 = 3---> b = 5
a = 2·5/5----> a = 2
c = -2 - 5 + 1-----> c = -6
94774
punti
Genius II
Fascio di parabole con asse di simmetria //asse y. Equazione dell'asse
x= [(1-7/2)/2] = - 5/4
Equazione del fascio:
y= a(x-1)(x+7/2)+1
Imponendo la condizione:
P(-5)=19
si ricava il valore del parametro a
19=a*(-6)(-3/2)+1
a=2
Quindi il polinomio è
2(x-1)(x+7/2)+1 = 2x²+5x-6
76754
punti
Genius II
@stefanopescetto purtroppo io ancora non ho fatto fasci di parabole etc, sono solo in seconda superiore, ma grazie mille lo stesso!!
Ok. Non sapendo la classe ho scelto la via più veloce. Allora segui il procedimento della Prof. Mg. Buona giornata
@stefanopescetto si scusatemi, avrei dovuto specificare! buona giornata anche a lei!
P(1) = 1;
P(-7/2) = 1;
P (- 5) = 19;
Devi sostituire alla x del polinomio P(x) i tre valori che ti da l'esercizio.
P(x) = a x^2 + b x + c
x = 1;
a + b + c = 1;
x = - 7/2;
a * (- 7/2)^2 + b * (- 7/2) + c = 1
49/4 a - 7/2 b + c = 1; mcm = 4;
49a - 14 b + 4 c = 4
x = - 5;
a * (-5)^2 + b * (-5) + c = 19
25 a - 5b + c = 19.
Abbiamo tre equazioni:
a + b + c = 1; (1)
49a - 14 b + 4 c = 4 (2)
25 a - 5b + c = 19; (3)
c = 1 - a - b; (1) sostituiamo nella (2) e nella (3)
49a - 14 b + 4 * (1 - a - b) = 4; (2)
49a - 14 b + 4 - 4a - 4b = 4; (2)
45a - 18b = 0, (2)
25 a - 5b + 1 - a - b = 19; (3)
24a - 6b = 18; (3)
abbiamo due equazioni con incognite a e b:
45a - 18b = 0, (2)
24a - 6b = 18; (3);
a = 18b / 45 = 2b/5 ; (2) sostituiamo a nella (3)
24 * (2b/5) - 6b = 18 ; (3)
48 b - 30b = 18 * 5; (3)
18 b = 18 * 5;
b = 5;
a = 2 b / 5 = 2;
c = 1 - a - b = 1 - 2 - 5 = - 6;
Polinomio:
P/x) = 2x^2 + 5x - 6.
Ciao @mujika
74863
punti
Genius II
@mg grazie mille, unica cosa nella prima a+b+c uguale ad uno perchè poi dice p(-7/2) uguale ad 1? Nel mio primo tentativo avevo messo a+b+c=0
@mujika leggi bene il testo. Dice: P(1) = P(-7/2) = 1; le prime due equazioni sono uguali a 1, tutte e due.
La terza P(-5) = 19. Ciao.
