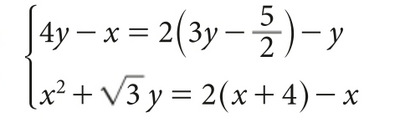Ciao a tutti. Stavo svolgendo questo esercizio ma mi sono bloccata.
Ho svolto le moltiplicazioni e isolato dalla prima la x (x=-y+5) e l'ho sostituita nella seconda ottenendo y^2+y(-9 + rad(3)) -12=0.
Mi sono calcolata poi il delta = 132 -18rad(3) ma non riesco ad andare avanti perchè non avendo fatto i radicali doppi non so come calcoalre la radice di questo valore.
Qualcuno può aiutarmi?
Grazie
164
punti
Livello 1
Dalla 1^:
4·y - x = 2·(3·y - 5/2) - y-----> x = 5 - y e ci siamo!
per sostituzione:
(5 - y)^2 + √3·y = 2·((5 - y) + 4) - (5 - y)
(y^2 - 10·y + 25) + √3·y = (18 - 2·y) - (5 - y)
(y^2 - 10·y + 25) + √3·y = 13 - y
y^2 + y·(√3 - 9) + 12 = 0 (hai sbagliato l'ultimo segno)
Δ = (√3 - 9)^2 - 48---> Δ = 36 - 18·√3
Siccome nella formula risolutiva compare √Δ e non vuoi applicare la formula del radicale doppio, vediamo se si può fare altrimenti....
Ricerchiamo v e w positivi, tali che:
√(36 - 18·√3) = √v - w
eleviamo al quadrato:
36 - 18·√3 = v - 2·√v·w + w^2
per confronto:
{v + w^2 = 36
{2·√v·w = 18·√3-----> w = 9·√3/√v
per sostituzione:
v + (9·√3/√v)^2 = 36----> v + 243/v = 36
soluzioni:
v = 27 ∨ v = 9
per v=27: w = 9·√3/√27= 3-----> √(36 - 18·√3) = √27 - 3 = 3·√3 - 3
per v=9: w = 9·√3/√9 = 3·√3------> √(36 - 18·√3) =3- 3·√3 (impossibile!)
Penso ora di essere arrivato alla conclusione!
94792
punti
Genius II
Vuoi qualche altra strada alternativa ai radicali doppi oppure vuoi sapere come risolvere radicali doppi?
94792
punti
Genius II
@lucianop alternativa.. non posso usare radicali doppi.
@lucianop quindi?
Fai prima ad imparare i radicali doppi secondo me. Un'altra alternativa per ora non la vedo.
