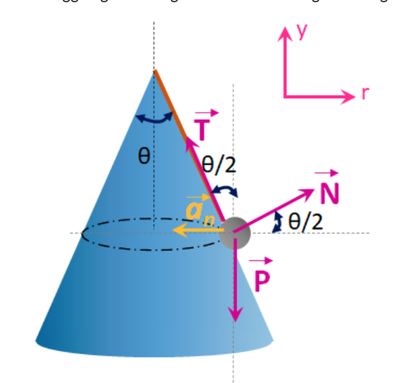
Salve, ecco un altro problema di fisica 1 che non riesco a risolvere.
Una massa puntiforme di $0.2 \mathrm{~kg}$ è appoggiata sulla superficie laterale, priva di attrito, di un cono di apertura di $120^{\circ}$ ed è trattenuto da un filo di lunghezza $L=50 \mathrm{~cm}$, il cui estremo è fissato al vertice del cono. La massa è posta in rotazione attorno all'asse del cono con velocità angolare costante di $6 \mathrm{rad} / \mathrm{s} .$ Controllare che con i dati forniti la massa rimane appoggiata al cono. Inoltre determinare la tensione del filo.
Ho provato a proiettare le forze su degli assi aventi come origine la massa stessa. Ho quindi:
Ncos(60)-Tsen(60)=macon "a" l'accelerazione centripeta sull'asse delle x. Per il secondo principio della dinamica.
sull'asse delle y, invece, ho proiettato la T: Tcos(60)
E la N: Nsen(60).
Poi ho sommato Nsen(60)+Tcos(60)=mg.
Adesso risolvo il sistema dato dalle due equazioni:
Le sommo e ottengo questa equazione:
N=m(a+g)-T[(1-radice(3))/2]*[2/(radice(3)+1)]
trovando T dalla seconda equazione
+T=[mg-Nsen(60)]/cos(60)
il problema è che il risultato non torna e non so dove ho sbagliato. T=3,68 N è il risultato corretto.
