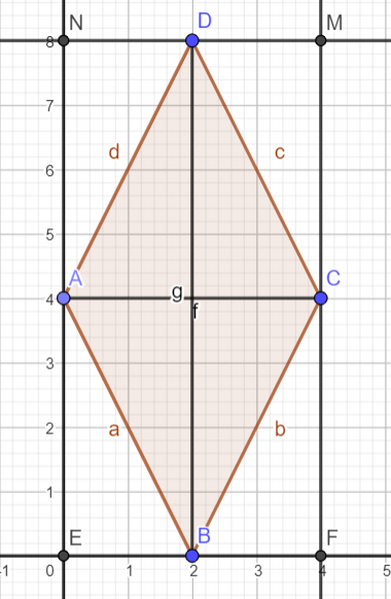
Disegna un rombo $A B C D$ e le sue diagonali. Traccia, per ogni vertice, la retta parallela alla diagonale opposta. Le quattro rette si incontrano a due a due nei punti $M, N, E, F$.
Dimostra che:
a. MNEF è un rettangolo;
b. ogni vertice del rombo è punto medio dei lati del rettangolo.
Buonasera, allego traccia e risoluzione dei tale dimostrazione
517
punti
Livello 2
Le diagonali di un rombo sono tra loro perpendicolari.
Allora le parallele tracciate sono tra loro perpendicolari e quindi EFMN è un rettangolo avendo i quattro angoli retti.
--
Considero le tre parallele NM, AC e EF tagliate dalle trasversali NE e DB.
Detto O il centro del rombo, abbiamo che DO=OB per le proprietà dei rombi. Allora per il teorema di Talete anche NA=AE e dunque A è punto medio.
Analogamente si dimostra che anche gli altri vertici sono punti medi.
Noemi
9874
punti
Livello 5
@n_f grazie mille
