Buongiorno potreste aiutarmi a risolvere questo quiz?
Si hanno due condensatori a facce piane e parallele identici e in serie. Se al secondo condensatore dimezzo la distanza tra le lastre, quanto vale il rapporto $\frac{C_{e q}}{C_1}$ ?
Grazie in anticipo per chi mi aiuterà!
21
punti
Livello 0
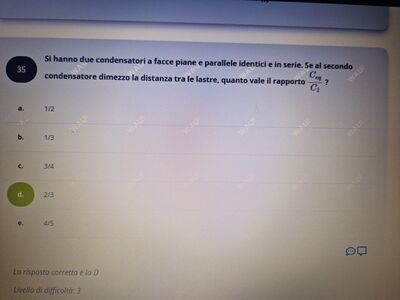
La capacità di un condensatore è legata alla distanza tra le lastre dalla formula:
$ C = S \epsilon_0 / d$
con $S$ superficie della lastra e $d$ distanza.
Ciò implica che capacità e distanza sono inversamente proporzionali: dimezzando la distanza, la capacità raddoppia.
Chiamiamo dunque $C_1$ e $C_2$ le capacità dei due condensatori. Per quanto detto $C_2 = 2 C_1$.
Essendo in serie, la capacità equivalente è:
$ C_{eq} = \frac{1}{\frac{1}{C_1}+\frac{1}{C_2}} = \frac{1}{\frac{1}{C_1}+\frac{1}{2C_1}} = \frac{1}{\frac{3}{2C_1}} = \frac{2}{3} C_1$
Quindi il rapporto richiesto è:
$ \frac{C_{eq}}{C_1} = \frac{2}{3}$
Noemi
9874
punti
Livello 5
@n_f Grazie mille per la spiegazione! Ora mi è tutto più chiaro, grazie ancora ❤️ Buona serata.
Figurati, in bocca al lupo per il test! 🙂
@n_f grazie di cuore!
@n_f 👍👍
C1 = C2 = 1
dimezzando la distanza , C2 raddoppia
C'2 = 2C2 = 2
Ceq = C1//C'2 = 1//2 = 2/3
Ceq/C1 = 2/3 /1 = 2/3
114459
punti
Genius II
Le capacità iniziali sono C1 e C1
La prima resta C1, la seconda é e S/d
e diventa C'2 = e S /(d/2) = 2e S/ d = 2 C1
La serie quindi si porta a Ceq = C1*2C1/(C1 + 2C1) = 2/3 C1
e infine Ceq/C1 = 2/3
47916
punti
Livello 7
@eidosm 👍👌👍
