REALTA E MODELLI Salto pericoloso
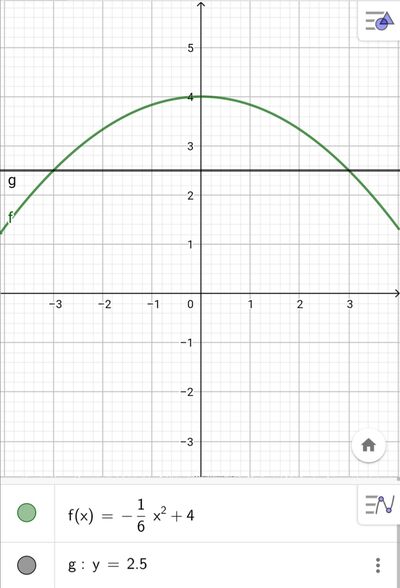
La traiettoria del pesce che spicca un salto nel sistema di riferimento della figura ha equazione
$$
y=-\frac{1}{6} x^{2}+4
$$
Verifica che riuscirà a entrare nella seconda boccia e calcola le coordinate del punto di impatto.
17
punti
Livello 0
L'intersezione della parabola che descrive la traiettoria del pesce con la retta di equazione y=2,5 ha come soluzioni x=-3 e x=3.
{y = 2,5
{y = - (1/6)*x² + 4
Sostituendo la prima equazione nella seconda otteniamo:
(1/6)*x² = 1,5
x² = 9
x= - 3 (ascissa del punto dove il pesce spicca il salto)
x= 3 (ascissa del punto di impatto)
Il pesce riesce a saltare dentro la seconda boccia.
Il punto di impatto ha coordinate (3 ; 2,5)
76753
punti
Genius II
ordinata di interesse :{y = 2,5 (*)
equazione parabola : {y = -x^2/6+4 (**)
sostituendo la (*) nella (**)
x^2/6 = (4-2,5)
x = √9 = ± 3,0
coordinate del punto di avvio : (-3 ; +2,5)
coordinate del punto di splash : (+3 ; +2,5)
114281
punti
Genius II
Vedi la mia risposta al link
http://www.sosmatematica.it/forum/postid/48528/
57383
punti
Genius I
