Problemi sul cerchio

Question

Buongiorno a tutti; vado a pubblicare alcuni problemi sul cerchio che non riesco a risolvere. Se qualcuno può e vuole aiutarmi, gliene sarò grato.

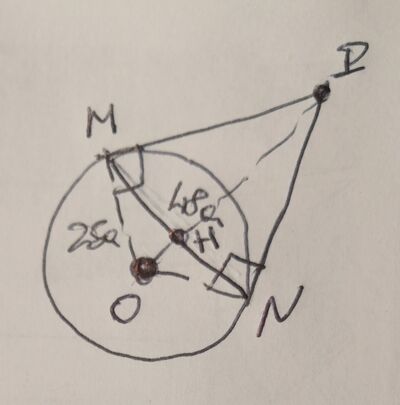
1) In un cerchio di raggio 2a tracciare la corda MN in modo che la somma di essa con la sua distanza dal centro O sia uguale ai 29/13 del raggio . Risposte : MN1 = 48/13a; MN2 = 224/65a

2) Trovare la misura della corda MN di un cerchio il cui raggio misura a, sapendo che la differenza fra la corda e la sua distanza dal centro è uguale al raggio . Risposta : 8/5 a

3) Condurre da un punto esterno P, una secante ad un cerchio di raggio 10a. Sapendo che la distanza fra il punto P ed il centro O del cerchio è 26a, e che la parte interna della secante è 16a, calcolare la lunghezza della parte esterna. Risposta : 8a (radice quadrata 10 -1).

4) I raggi di due cerchi concentrici sono rispettivamente 10a e 17a. Si conduca una retta in modo che la corda determinata su di essa dalla circonferenza minore sia uguale ai 2/5 di quella maggiore. Si determinino la distanza della retta dal centro e la lunghezza delle due corde. Risposta : d= 8a; c1 = 12a; c2 = 30a.

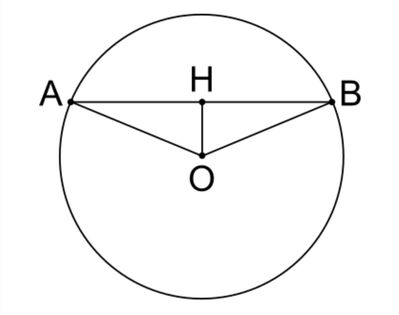
5) E' dato un cerchio di raggio 13a e un punto A (interno) che dista dal centro 5a. Condotta per A una corda lunga 25a, calcolare le lunghezze dei segmenti in cui la corda resta divisa dal punto A. Risposta : 9a; 16a

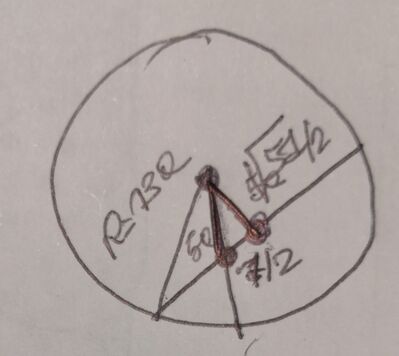
6) Il raggio di un cerchio è 25a ed una sua corda misura 48a. Detto P il punto d'intersezione delle due tangenti al cerchio negli estremi della corda, determinare la distanza fra il punto P ed il centro O del cerchio dato. Risposta : PO= 625/7a

7) Un punto interno ad un cerchio di raggio 20a, divide una corda in due segmenti il cui prodotto è 300a^2. Trovare la distanza del punto dal centro. Risposta : 10a

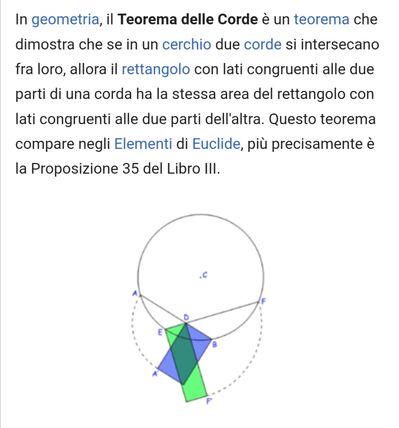
8) Due corde di un cerchio si tagliano in un punto tale che divide la prima in due segmenti lunghi rispettivamente 12a e 8a. Sapendo che la seconda corda è lunga 22a, trovare le misure dei due segmenti in cui viene divisa dalla prima. Risposta : 16a; 6a.

Grazie a tutti anche per solo uno o qualche problema che vorrete risolvere.

Autore

Risposta

Beppe

(@beppe)

1502 punti

livello:

Livello 1

1268 Risposte
466 3 796

17/12/2022 15:57

StefanoPescetto · Accepted Answer

[attach]32261[/attach] Ciao Beppe,  Rispondo per cominciare ai primi OTTO esercizi.  Osservando la figura, si capisce che il triangolo OAB è isoscele. La distanza della corda dal centro della circonferenza è quindi l'altezza relativa alla base di un triangolo isoscele ed è quindi anche mediana (divide la corsa in due parti uguali), bisettrice, asse del segmento 1) Raggio = 2a  Corda = 2x    Imponendo la condizione richiesta: AB + OH = (29/13)*2a Quindi: 2x + radice (4a² - x²) = (58/13)*a   Da cui si ricava: x= (24/13)*a  v  x= (112/65)*a   Avendo la corda lunghezza 2x, le soluzioni sono: AB=(48/13)*a  v  AB=(224/65)*a   Es2)  Facendo sempre riferimento alla figura, indicando con 2x la lunghezza della corda, la condizione richiesta è soddisfatta se: 2x - radice (a² - x²) = a   Da cui si ricava: x=(4/5)*a Quindi AB= (8/5)*a   ESERCIZIO 3) La distanza del punto P dal centro della circonferenza è l'ipotenusa di un triangolo rettangolo avente come cateti il raggio della circonferenza e la misura della tangente (vedi figura allegata ieri)   Indichiamo con T il punto di tangenza.  PT= radice (PO² - R²) = radice [a²(26² - 10²)] = 24a   Applicando il teorema della secante e della tangente (vedi ieri), indicando con x la parte esterna della secante, si ricava: (16a + x) /24a = 24a/x   Da cui si ricava: x= 8a* [radice (10) - 1]   Esercizio 4) Indichiamo con 5x e 2x le due corde, essendo la distanza dal centro la stessa, vale la relazione: (L1, L2 = lunghezza delle corde)    radice [R1² - (L1/2)²] = radice [R2² - (L2/2)²]   Sostituendo i valori numerici otteniamo: radice (100a² - x²) = radice [17²*a² - (25/4)*x²]   Da cui si ricava l'unico valore accettabile: x= 6a   Le due corde hanno quindi lunghezza: L1= 2x = 12a  ;  L2= 5x = 30a   Esercizio 5) [attach]32274[/attach] Conoscendo la lunghezza del raggio e della corda, determino la distanza di quest'ultima dal centro.    D= radice (13²a² - 12,5² a²) = a*radice (51)/2   La distanza di A da O è l'ipotenusa di un triangolo rettangolo avente come cateti la distanza della corda dal centro e la distanza tra A e il piede della perpendicolare condotta dal centro O sulla corda.  Utilizziamo il teorema di Pitagora per determinare questa distanza:   d= radice (5²a² - (51/4)*a²) = (7/2)*a   Quindi il punto A divide la corda in due segmenti di lunghezza: L1= (25/2)a + (7/2)a = 16a L2= (25/2)a - (7/2)a = 9a   Esercizio 6) [attach]32275[/attach] Indichiamo con T la lunghezza dei segmenti di tangenza e con x la distanza del punto O dal centro.  Possiamo esprimere l'area del triangolo rettangolo OMP come semiprodotto dei cateti o semiprodotto della base (OP) per altezza (MH).  Quindi:   {25a*T/2 = (x*24a)/2 {T²+625a² = x² (ipotenusa = somma dei quadrati dei cateti)    {T=(24/25)x   Sostituendo il valore di T nella seconda equazione si ricava:   (49/625)x²=625a² Da cui: x= 625a /7   Esercizio 8) [attach]32280[/attach] Quindi essendo la prima corda divisa in due parti di lunghezza 12a e 8a ed essendo la seconda corda lunga 22a, quest'ultima sarà divisa in due parti il cui prodotto è 96a² {x+y= 22a {xy= 96a²   Quindi: x=6a;y=16a Le due corde sono lunghe 6a e 16a   Esercizio 7) Usi il teorema della corda enunciato nel punto precedente  La seconda corda è il diametro della circonferenza passante per il punto. Indicando con x, y le due parti in cui è diviso il diametro, risulta: {x+y= 40a {x*y= 300a²   Da cui si ricava: x=30a e y=10a. Essendo il raggio R=20a, la distanza del punto dal centro O della circonferenza è 10a

[Risolto] Problemi sul cerchio

Domande