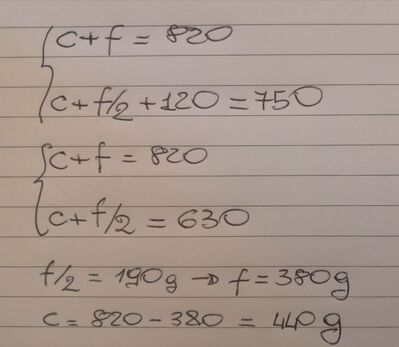[Risolto] Problemi matematica sistemi

PROCEDIMENTO PER L'IMPOSTAZIONE DEL PROBLEMA
Un esercizio è un testo che descrive in narrativa una situazione problematica.
Impostare il problema significa costruirne un modello matematico a partire dalla descrizione, cioè assegnare un nome simbolico a ciascuna entità rilevante e poi esprimere in termini di questi simboli le relazioni fra le entità.
Risolvere il problema impostato significa manipolare il modello fino a isolare, se possibile, i simboli dei risultati richiesti; se è stato possibile allora sostituire i valori noti ai simboli che li rappresentano e valutare le risposte.
------------------------------
NEL CASO IN ESAME
---------------
A) Assegnare nomi simbolici
Le entità rilevanti sono masse, in grammi: ciotola, farina, zucchero.
I valori noti sono la massa di zucchero e le letture di pesate: prima, seconda.
Il risultato richiesto è la massa della ciotola, che perciò merita il simbolo "x".
Poi nomino "y" la massa iniziale di farina e "z" quella di zucchero.
Infine nomino "p" la prima lettura e "s" la seconda.
---------------
B) Esprimere le relazioni
1) "... una ciotola che contiene della farina e legge 820 grammi" ≡
≡ x + y = p
2) "Dimezzando la quantita di farina" ≡ y/2 +
3) "aggiungendo 120 grammi di zucchero" ≡ + z
4) "legge 750 grammi" ≡ x + y/2 + z = s
---------------
C) "Quanto pesa la ciotola?" ≡ Determinare x
* (x + y = p) & (x + y/2 + z = s) ≡
≡ (y = p - x) & (x + (p - x)/2 + z = s) ≡
≡ (y = p - x) & (x = 2*s - p - 2*z)
sostituendo i valori dati si ha
* x = 2*s - p - 2*z =
= 2*750 - 820 - 2*120 = 440 g
che è proprio il risultato atteso.

Indichiamo con

c=peso in grammi ciotola 

f=peso in grammi di farina 

La ciotola pesa 440g

@Shanks

c+f/2+120 = 750 g

2c+f = (630*2) g

c+f = 820 g

sottraendo l'una dall'altra

c = 440 g  

@shanks

Ciao e benvenuto.

Nei problemi di questo tipo devi subito inquadrare le incognite. Le puoi chiamare come ti pare e ti piace, leggere attentamente il problema ed interpretarlo correttamente.

x= peso della ciotola

y= peso della farina

Quindi scrivi:

{x+y=820

{x+y/2+120=750

Lo zucchero è quindi un distraente del problema (perché a questo punto poteva essere qualsiasi cosa, anche un sasso di 120 g). Dopodiché è fatta! 

eddai, semplicissimo

farina + ciotola = 820
(1/2) farina + 120 + ciotola = 750

f + c = 820
(1/2) f + 120 + c = 750

(f=380, c=440)