problemi geometria calcolo

Question

:(ho delle difficoltà sul risolvere questi due problemi....

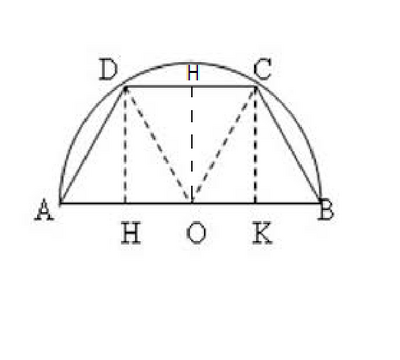
1) In una CFR traccia un diametro e una corda a esso parallela. La corda misura 24 m e dista dal centro 9 m. Calcola l'area del trapezio isoscele che viene a generarsi collegando fra loro il diametro e la corda e l'area del ritaglio ottenuto estraendo dal cerchio il trapezio.

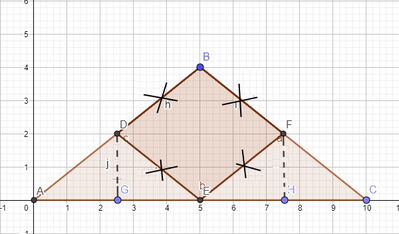
2) La base e il lato di un triangolo isoscele misurano rispettivamente 60 cm e 50 cm. Fissando i punti medi di ciascun lato, si ottiene internamente un rombo. Calcolare la superficie del rombo.

ho provato il primo e poi non c'è l'ho fatta a completarlo perché mi dava risultati impossibili poi ho provato con il secondo problema e stessa cosa, grazie per chi mi dia una mano

Autore

Risposta

serenaikishima

(@serenaikishima)

8 punti

livello:

Livello 0

5 Risposte
5 0 0

08/03/2022 21:03

remanzini_rinaldo · Accepted Answer

1 [attach]17877[/attach] corda DC = 24 semicorda CH = 24/2 = 12 distanza OH = 9 raggio OC = 3√3^2+4^2 = 3*5 = 15 cm  diametro AB = 2*OC = 30 cm  area trapezio At = (30+24)*9/2 = 243 cm^2 area del cerchio Ac = 3,1416*15^2 =706,8 cm^2 differenza aree Ac-A = 706,8-243 = 463,8 cm^2   2 basta tracciare la figura e ci si rende conto che il triangolo si compone di 4 triangoli uguali , due dei quali formano il rombo che ha, quindi, un'area uguale alla metà di quella del triangolo base. altezza h del triangolo = 10√5^2-3^2  = 10*4 = 40 cm  area del rombo = 60*40/4 = 60*10 = 600 cm^2

StefanoPescetto · Answer

@serenaikishima  [attach]17888[/attach] La diagonale maggiore del rombo è congruente all'altezza del triangolo isoscele. Quindi: D= radice (50² - 30²) = 40 cm La diagonale minore risulta invece metà della base del triangolo isoscele. Infatti  d= 60 - 15 - 15 = 30 cm   Puoi quindi calcolare l'area del rombo  A= (d*D) /2

BobOclat · Answer

prima calcoli il raggio della crf(24/2)^2 + 9^2 = r^2r = 15poi l'area del trapezios = (24 + 15*2 + 24) * 9 / 2 s = 351 poi l'area del cerchios = 3.14 * 15^2s = 706.5 poi fai la differenza fra le aree

[Risolto] problemi geometria calcolo

Domande