Problemi funzioni goniometriche

Question

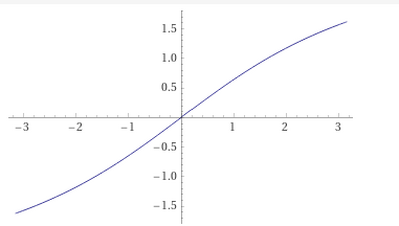
599. Considera la funzione f(x) = a tan (bx)

a. Determina a e b con b>0, in modo che il suo periodo sia 2pigreco e che il suo grafico passi per il punto di coordinate (-pigreco/2, -3)

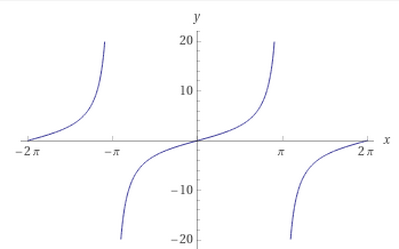
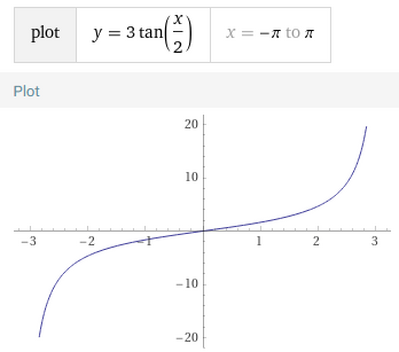
b. Traccia il grafico della funzione y=f(x) in corrispondenza dei valori a e b trovati

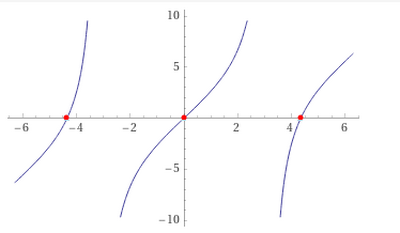
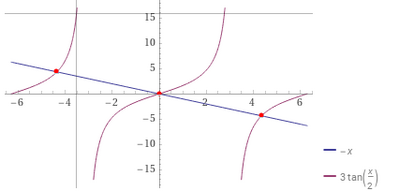
c. Servendoti del grafico tracciato, stabilisci graficamente il numero delle soluzioni dell'equazione f(x) + x = 0 nell'intervallo [-2pigreco, pigreco]

d. Stabilisci se l funzione è invertibile nell'intervallo [-pigreco, pigreco] e in caso affermativo determina l'espressione analitica della funzione inversa.

SOLUZIONE [ a. a=3, b=1/2; c. 3 soluzioni; d. f(-1)(x) =2arctan x/3 ]

Autore

Risposta

giorgio_melone

(@giorgio_melone)

38 punti

livello:

Livello 0

50 Risposte
23 0 27

13/02/2023 15:01

lorenzo_belometti · Accepted Answer

Sia la funzione f(x) =a. tan(bx)$ La generica funzione f(x) = a. tan(bx+ varphi )$ ha periodo T =  pi / |b|$ Dai dati riportati si ha $ T = frac { pi }{b} = 2 pi e quindi b =  frac {1}{2} Per trovare a usiamo gli altri dati forniti dal problema f(- pi /4) = a. tan( frac {1}{2}.  frac {- pi }{2}) =-3$ $ a. tan( frac {- pi }{4}) =-3$ La funzione tangente è dispari quindi tan(-x) = -tan(x)$ $ -3 = a. (-1)$  a = 3$ Il grafico della funzione f(x) = 3tan(x/2)$ risulta [attach]37655[/attach]   La funzione f(x) + x=0$ presenta tre zeri [attach]37657[/attach] Il periodo della funzione non cambia. È possibile trovare gli zeri anche in questo modo: $3tan(x/2) = -x dove gli zeri sono le intersezioni dei grafici delle due funzioni elementari nell'intervallo indicato dal testo. [attach]37662[/attach] La funzione $3tan(x/2)$ è invertibile nell'intervallo indicato, come si vede nella figura   [attach]37660[/attach]   La funzione inversa allora esiste e si trova come  y = 3tan(x/2)$  tan^{-1}(y/3) = x/2$  x = 2tan^{-1}(y/3)$. Sostituendo x con y si ottiene y =2tan^{-1}(x/3)$. [attach]37664[/attach]

[Risolto] Problemi funzioni goniometriche

Domande