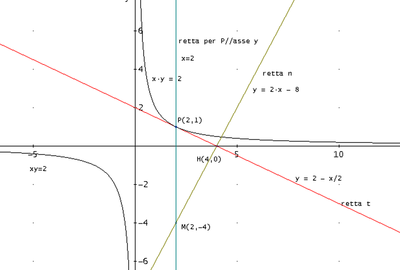
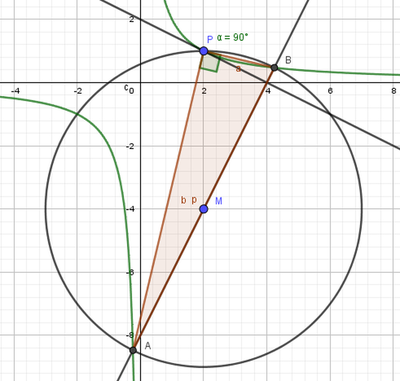
Scrivi l’equazione dell’iperbole equilatera avente per asintoti gli assi cartesiani e passante per il punto P(2,1) E determina l’equazione della retta t, tangente in P all’iperbole. Indica con H il punto di intersezione con l’asse x della retta t e scrivi l’equazione della retta n passante per H e perpendicolare a t. Detto A e B i punti di intersezione della retta n con l’iperbole, verifica che il punto medio M di AB appartiene alla retta passante per P parallela all’asse y e che il triangolo APB è rettangolo in P. Determina infine l’equazione della circonferenza circoscritta ad APB
GRAZIE MILLE