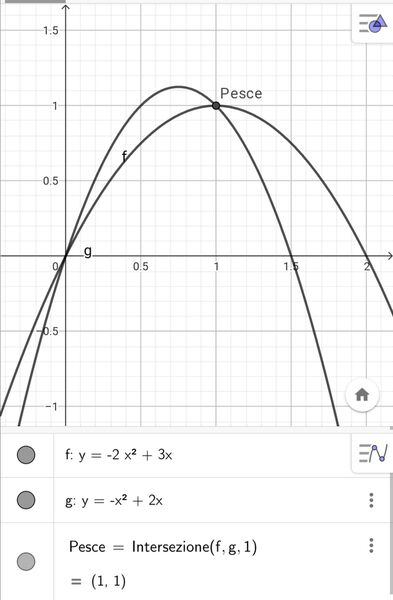
Gatto goloso Felix è un gatto goloso che, fiutando l'odore del pesce posto sul bordo della dispensa, spicca un salto per raggiungerlo. La traiettoria del gatto è una parabola di equazione
$$
y=-\frac{1}{5}\left(1+m^2\right) x^2+m x, \quad \text { con } m \in R ^{+} .
$$
a. Dimostra che $m$ rappresenta il coefficiente angolare della tangente alla parabola in $O$.
b. Dimostra che vi sono due valori distinti di $m$ per i quali Felix riesce proprio a raggiungere il pesce e disegna le due possibili traiettorie.
c. Qual è la massima altezza raggiunta da Felix nei due casi?
Non riesco a fare la domanda A. qualcuno riesce ad aiutarmi