Problema Trigonometria n. 180

Question

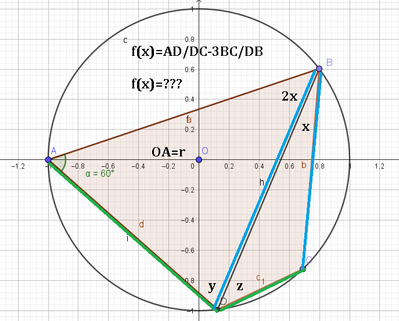
È dato il quadrilatero A B C D inscritto in una circonferenza di raggio r. L'angolo in A è di  frac { pi }{3}, quello in B è tale che A  widehat {B} D è doppio di D  widehat {B} C. Poni D  widehat {B} C=x e determina l'espressione analitica della funzione f(x)= frac { overline {A D}}{ overline {D C}}-3  frac { overline {B C}}{ overline {D B}} . Trova per quali valori di x si ha f(x)< sqrt {3}.  left [f(x)=2  sin (x- frac { pi }{6}),  operatorname {con} 0<x< frac { pi }{3} ; 0<x< frac { pi }{6} right ]  [attach]69941[/attach] Ho provato a risolvere ma non mi escono i risultati

LucianoP · Accepted Answer

[attach]69959[/attach] Con riferimento alla figura riportata sopra, utilizziamo: a) la proprietà dei quadrilateri inscritti in una circonferenza: "Un quadrilatero può essere inscritto in una circonferenza se e solo se due angoli opposti sono supplementari" b) Il teorema della corda:"la lunghezza di una corda AB di una circonferenza di raggio r è data dal doppio prodotto del raggio per il seno di uno degli angoli alla circonferenza che insistono sulla corda" {y + z + 2·x + x = pi {y = pi - (pi/3 + 2·x) risolvo ed ottengo: [y = 2·(pi - 3·x)/3 ∧ z = (pi - 3·x)/3] (in grassetto quello che ci interessa) Quindi ci prepariamo i termini: ΑD = 2·r·SIN(2·x) DC = 2·r·SIN(x) ΒC = 2·r·SIN((pi - 3·x)/3) DΒ = 2·r·SIN(pi/3) f(x)=2·r·SIN(2·x)/(2·r·SIN(x)) - 3·(2·r·SIN((pi - 3·x)/3))/(2·r·SIN(pi/3)) semplificando: f(x) = 2·COS(x) + 2·√3·SIN(x - pi/3) tenendo conto che: SIN(x - pi/3) = SIN(x)·COS(pi/3) - SIN(pi/3)·COS(x) SIN(x - pi/3) = SIN(x)/2 - √3·COS(x)/2 si ha: f(x)= 2·COS(x) + 2·√3·(SIN(x)/2 - √3·COS(x)/2) f(x)=√3·SIN(x) - COS(x) Utilizzando il metodo dell'angolo aggiunto si arriva quindi alla funzione attesa: f(x)=Α·SIN(x + φ) = 2·SIN(x - pi/6)

[Risolto] Problema Trigonometria n. 180

Domande