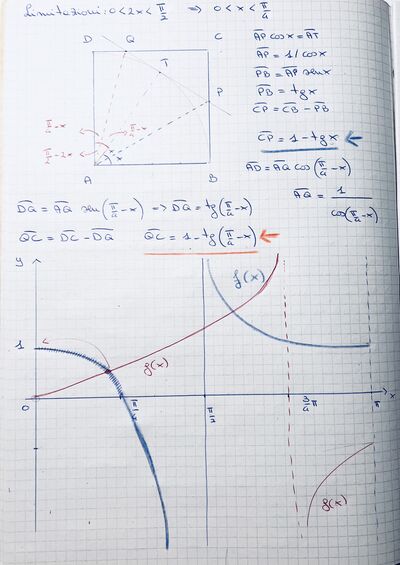
[Da risolvere solo con formule del triangolo rettangolo della trigonometria e senza calcolatrice]
Dato un quadrato ABCD di lato 1, considera sull'arco di circonferenza di centro A e raggio AB, contenuto nel quadrato, un punto T in modo che l'angolo TAB misuri 2x. Traccia la tangente all'arco di circonferenza passante per T e chiama P e Q i punti in cui essa interseca, rispettivamente, le rette BC e CD.
Determina l'espressione analitica
delle funzioni:
a. y = f (x) = CP
b. y = 8(x) = CQ
e traccia i loro grafici nell'intervallo [0, ], mettendone in evidenza il tratto relativo al problema.
[Risultati nell’immagine allegata]