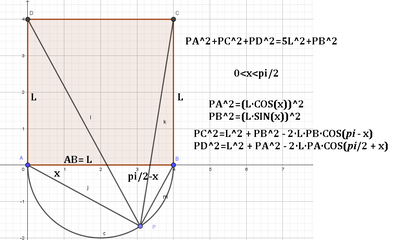
303 Dato un quadrato $A B C D$ di lato $l$, costruisci, esternamente a esso, la semicirconferenza di diametro $A B$ ecoses dera su di essa un punto $P$. Determina la posizione di $P$ affinché sia verificata la relazione:
$$
\overline{P A}^2+\overline{P C}^2+\overline{P D}^2=5 l^2+\overline{P B}^2 \quad\left[\text { Ponendo } P \widehat{A} B=x, \text { si giunge all'equazione } 3 \sin ^2 x-4 \sin x \cos x+\cos ^2 x=1\right. \text {. }
$$
11
punti
Livello 0
Non riesco a leggere bene l'equazione espressa nella soluzione in blu.
Io arrivo a scrivere come equazione: 4·SIN(x)·COS(x) - 2·SIN(x)^2 - 1 = 0
Con riferimento alla figura di sopra ottengo:
PA^2=(L·COS(x))^2 = L^2·COS(x)^2
PC^2=L^2 + (L·SIN(x))^2 - 2·L·L·SIN(x)·COS(pi - x) = 2·L^2·SIN(x)·COS(x) + L^2·SIN(x)^2 + L^2
PD^2=L^2 + (L·COS(x))^2 - 2·L·L·COS(x)·COS(pi/2 + x) = L^2·COS(x)^2 + 2·L^2·SIN(x)·COS(x) + L^2
Al secondo membro= 5·L^2 + L^2·SIN(x)^2
Poi ottengo quello che ti ho detto nel commento...
94778
punti
Genius II
