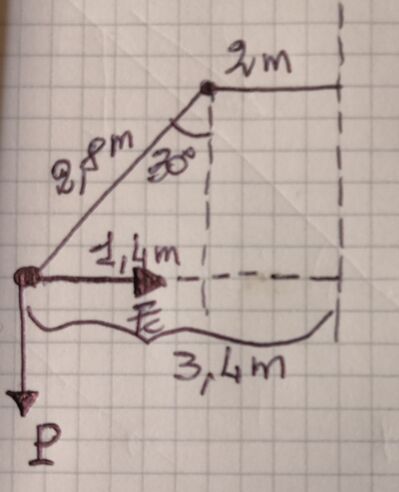
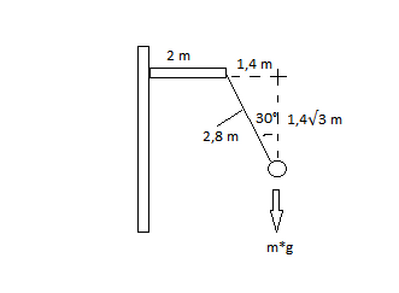
Una giostra con i seggiolini appesi a delle catene ha dei supporti orizzontali che distano 2,0 m dall’asse di rotazione. all’estremo di questi supporti sono vincolate le catene, lunghe 2,8 m. Durante il movimento di rotazione uniforme della giostra, i seggiolini si trovano a una distanza di 3,4 m dall’asse di rotazione
Determina la velocità angolare della giostra (1,3 rad/s)
determina il periodo del moto (4,9 s)
determina la velocità dei seggiolini (4,4 m/s)
grazie mille.