Problema su trapezio scaleno

@Beppe 

Allora è la base minore che supera di 6 cm l'altezza...

Ciao Beppe, 

A quel punto il problema è finito.

[(2b+24)*(b-6)]/2 = 1440

Da cui si ricava:

b=36 cm

H=30 cm

B=36+24= 60 cm

Si dimostra (corollario del Teorema di Talete) che:

In un qualsiasi trapezio il segmento congiungente i punti medi dei lati risulta essere // alle basi e pari alla metà della loro somma.

Dim:

La parallela alle basi del quadrilatero, passante per il punto medio del lato AB, interseca il lato DC nel suo punto medio N. (Talete) 

I triangoli CNO e CDA sono simili (3 angoli congruenti) con rapporto di similitudine k=1/2  => NO = (1/2)*AD

Analogamente sono simili i triangoli AMO e ABC con rapporto di similitudine k=1/2 => MO = (1/2)*BC

Allora: MN = (1/2)*(AD+BC) 

***********************************. 

Quindi:

B= 60 cm ; b= 36 cm ; b+B= 96 cm  =>

=> MN = 96/2= 48 cm

 Le basi di un trapezio differiscono fra loro di 24 cm e la base minore  b  supera di 6 cm l'altezza. Trovare la misura della congiungente i punti medi dei lati non paralleli, sapendo che l'area della superficie del trapezio è di cm^ 1440. Risposta cm 48

A = 1440 = (b+12)*(b-6) = b^2+6b-72

1512-b^2-6b = 0

b = (6-√36+1512*4)/-2 = (6-78)/-2 = 36 cm

B = b+24 = 36+24 = 60 cm 

detta x la distanza A'H si ha K'B' = 24-x

A'B' = b+x/2+(24-x)/2 = b+12 = b+(B-b)/2 

2A'B' = 2b-b+B = B+b 

L = A'B' = (B+b)/2 = 96/2 = 48 cm

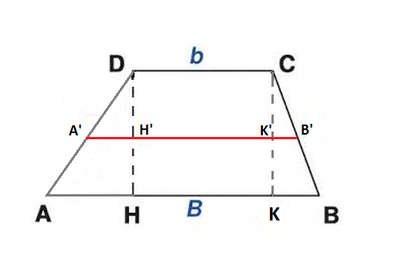
Nel trapezio di basi a < b e altezza h l'area S è il prodotto fra l'altezza e la media m delle basi quindi la richiesta media delle basi ("la congiungente i punti medi dei lati" obliqui) si ricava da
* S = h*(a + b)/2 = h*m ≡ m = S/h = 1440/h
Per ottenere il risultato atteso (m = 48) occorre che sia h = 30.
---------------
"Le basi di un trapezio differiscono fra loro di 24 cm" ≡ b = a + 24
"la base maggiore supera di 6 cm l'altezza" ≡ b = h + 6
Quindi
* (b = a + 24) & (b = h + 6) & (m = 1440/h) & (0 < a < b) ≡
≡ (h = a + 18) & (m = 1440/(a + 18)) & (b = a + 24) & (a > 0)
fra le infinite possibili soluzioni ce ne sono solo 23 in numeri naturali, e fra queste, quella del risultato atteso
* (a = 12) & (b = 36) & (h = 30) & (m = 48)
---------------
DETTAGLI
1440 ha 36 divisori naturali
* {1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 32, 36, 40, 45, 48, 60, 72, 80, 90, 96, 120, 144, 160, 180, 240, 288, 360, 480, 720, 1440}
che, diminuiti di 18 per avere i possibili "a" interi, danno
* {- 17, - 16, - 15, - 14, - 13, - 12, - 10, - 9, - 8, - 6, - 3, - 2, 0, 2, 6, 12, 14, 18, 22, 27, 30, 42, 54, 62, 72, 78, 102, 126, 142, 162, 222, 270, 342, 462, 702, 1422}
fra cui ci sono solo 23 possibili "a" naturali
* {2, 6, 12, 14, 18, 22, 27, 30, 42, 54, 62, 72, 78, 102, 126, 142, 162, 222, 270, 342, 462, 702, 1422}
fra cui c'è a = 12 che risolve l'esercizio nei termini desiderati dall'autore.