[Risolto] Problema su circonferenze

Ciao,

Vediamo innanzitutto la simmetria del problema e ragioniamo su di essa:

Le circonferenze che chiamo $s$ ed $r$ hanno rispettivamente i seguenti centri:

$P_{s}(x_{s},0)$

$P_{r}(x_{r},0)$

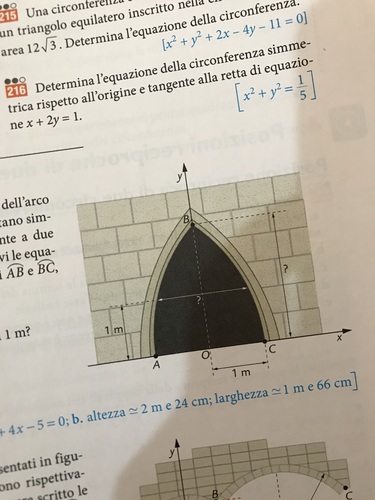
Supponiamo $s$ passante per $C(1,0)$ e $r$ passante per $A(-1,0)$

Ora sapendo che il le circonferenze hanno raggio $r=3m$

Avremo che:

$\overline{P_{s}C}=3m$ e $\overline{P_{r}A}=3m$ 

Ora calcolando la distanza tra i 2 punti ricaviamo le coordinate x dei rispettivi centri:

$\overline{P_{s}C}=|1-x_{s}|=3$

$x_{s}=-2$

$\overline{P_{r}A}=|x_{r}+1|=3$

$x_{r}=2$

Ora ricordando l'equazione di una circonfernza conoscendo centro e raggio:

$(x-x_{c})^{2}+(y-y_{c})^{2}=r^{2}$

Nel nostro caso:

$s: (x+2)^{2}+(y)^{2}=9$

$r: (x-2)^{2}+(y)^{2}=9$

Scriviamole in forma cononica:

$s: x^{2}+y^{2}+4x-5=0$

$r: x^{2}+y^{2}-4x-5=0$

Punto 1)

Per calcolare l'altezza troviamo prima l'intersezione tra le circonferenze:

$x^{2}+y^{2}+4x-5=x^{2}+y^{2}-4x-5$

Che ha soluzione per $x=0$

Sostituiamo il valore $x=0$ in una delle due equazioni ottenendo:

$0^{2}+y^{2}+4(0)-5=0$

$y^{2}-5=0$

Che ha soluzioni: $y=+/-\sqrt{5}$

Siamo interessati alla soluzione positiva cioè al punto $B(0,\sqrt{5})$ la coordinata y coincide banalmente con l'altezza del arco.

Quindi $h=\sqrt{5}m\approx2m24 cm$

Punto 2)

Per calcolare la distanza tra gli archi ad un metro di altezza troviamo il punto di intersezione tra la retta $y=1$ e le due circonferenze:

Procediamo:

Partiamo da $s$

$x^{2}+1^{2}+4x-5=0$

$x^{2}+4x-4=0$

Che ha soluzioni:

$x=-2+/-\sqrt{8}$

Siamo interessati alla soluzione positiva per cui consideriamo solo $x=-2+\sqrt{8}$

$x^{2}+1^{2}-4x-5=0$

$ x^{2}-4x-4=0$

Che ha soluzioni:

$x= 2+/-\sqrt{8}$

In questo caso siamo interessa alla soluzione negativa:

$x= 2-\sqrt{8}$

La distanza ad un metro da terra che chiamiamo $d$ si ottiene calcolando il valore assoluto della differenza dei valori trovati per cui:

$d=|2-\sqrt{8}-(-2+\sqrt{8})|$

$d=|4-2\sqrt{8}|$

$d\approx1m 66cm$

Cominciamo scrivendo le equazioni delle due circonferenze.

Sappiamo che entrambe hanno il centro sull'asse $ x $, da cui il centro avrà ordinata $ y_C = 0 $. Il raggio è, per entrambe $ r = 3 $.
In generale, quindi, le due equazioni avranno la forma
$ (x-x_C)^2 + y^2 = 3^2 $
$ (x-x_C)^2 + y^2 = 9 $

Sappiamo che la circonferenza di "destra" passa per il punto $ (1,0) $ (ce lo suggerisce la figura), quindi sostituiamo nell'equazione:
$ (1-x_C)^2+0 = 9 \rightarrow 1-2x_C + x_C^2 = 9 \rightarrow x_C^2 -2x_C -8 = 0 \rightarrow (x_C -4)(x_C+2) = 0 $
che ci dà due soluzioni: $ x_C = 4 $ oppure $ x_C = -2 $
dato che stiamo ragionando sulla circonferenza di destra, non ha senso che $ x_C = 4 $, quindi avremo $ x_C = -2 $
L'equazione della circonferenza di destra è quindi $ (x+2)^2+y^2 = 9 $.

Analogamente facciamo per la circonferenza di sinistra, che passa per $ (-1;0) $:
$ (-1-x_C)^2+0 = 9 \rightarrow 1+2x_C + x_C^2 = 9 \rightarrow x_C^2 +2x_C -8 = 0 \rightarrow (x_C -4)(x_C-2) = 0 $ che ci dà $ x_C=4 $, $ x_C = 2 $. In questo caso scegliamo $ x_C = 2 $ per simmetria delle due circonferenza (che deriva dall'ipotesi di simmetria dell'arco data nel problema). Quindi l'equazione sarà $ (x-2)^2+y^2 = 9 $

L'altezza dell'arco gotico è l'altezza del punto $ B $, che è intersezione delle due circonferenze. Possiamo calcolare questo punto facendo l'intersezione tra le due circonferenze, ovvero mettendone a sistema le equazioni; questo sarebbe il procedimento "generale". Possiamo anche osservare che in questo caso il punto sta sull'asse $ y $, quindi sarà del tipo $ (0;y_B) $.Infatti, oltre ad essere il punto di intersezione tra le due circonferenze, $ B $ è il punto di intersezione tra una circonferenza e l'asse $ y $, che è molto più facile da calcolare! Prendiamo ad esempio la circonferenza di destra e proviamo a sostituire questo punto nella sua equazione:
$ (0+2)^2 + y_B^2 = 9 \rightarrow y_B^2 = 5 \rightarrow y_B = \pm \sqrt{5}$.
Il punto $ B $ sta dalla parte positiva dell'asse $ y $, quindi prendiamo $ y_B = + \sqrt{5}$ che ci dà il punto $ (0; \sqrt{5}) $. La distanza tra il punto $ B $ e l'origine è $ \sqrt{5} $, che è anche l'altezza dell'arco: $ \sqrt{5} \ m = 2.24 \ m $.

Per calcolare la larghezza dell'arco ad una altezza di $ 1 \ m $, possiamo calcolare la retta che taglia l'arco ad altezza $ 1 $, calcolare l'intersezione di questa con le due circonferenze e calcolare la distanza tra questi punti. Forse c'è un metodo più rapido, ma sinceramente è l'unico che mi viene in mente.
La retta da considerare è una retta orizzontale che passa per il punto $ (0;1) $, quindi $ y = 1 $. Calcoliamo l'intersezione con la circonferenza di destra:
$ \begin{cases}
y = 1 \\ (x+2)^2+y^2 = 9
\end{cases} $
$ \begin{cases}
y = 1 \\ (x+2)^2+1^2 = 9
\end{cases} $
$ \begin{cases}
y = 1 \\ x^2 + 4x + 4 +1 - 9 = 0
\end{cases} $
risolviamo $ x^2 +4x -4 = 0 $:
$ x_{1,2} = \frac{-4\pm \sqrt{4^2-4(1)(-4)} }{2} = \frac{-4\pm \sqrt{16+16}}{2} = \frac{-4 \pm \sqrt{32}}{2} = \frac{-4 \pm 4 \sqrt{2}}{2} = -2 \pm 2\sqrt{2}$.
Abbiamo ovviamente due soluzioni, che corrispondono alle due intersezioni della retta con la circonferenza di destra. A noi, ovviamente, interessa quella positiva quindi il punto è $ E = (-2+2\sqrt{2}; 1) $.
Allo stesso modo per l'equazione della circonferenza di sinistra, dove ci ritroveremo a risolvere l'equazione di secondo grado $ x^2-4x-4 = 0 $, che ha soluzioni $ x_{1,2} = 2 \pm 2\sqrt{2} $; sempre per simmetria scegliamo $ 2-2\sqrt{2} $ (che si ottiene dal punto $ E $ cambiando di segno). Il punto che abbiamo trovato è quindi $ F = (2-2\sqrt{2}; 1) $.

Siamo pronti per calcolare la distanza. Dato che i due punti hanno la stessa ordinata, basta calcolare la differenza delle ascisse e farne il modulo:
$ d = | x_E -x_F| = |-2+2\sqrt{2} - (2-2\sqrt{2})| = |-2+2\sqrt{2} -2+2\sqrt{2}| = |-4+4\sqrt{2}| = -4 + 4 \sqrt{2} = 1.66 \ m$.

ciao volevo sapere come si chiama questo libro