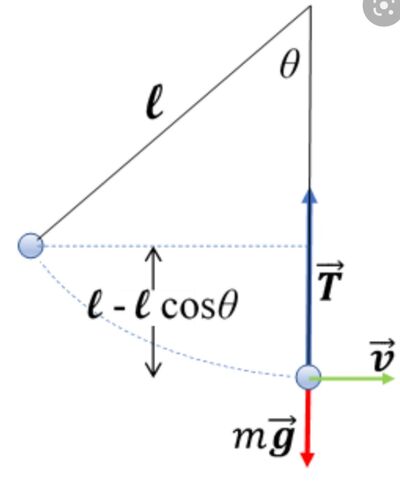
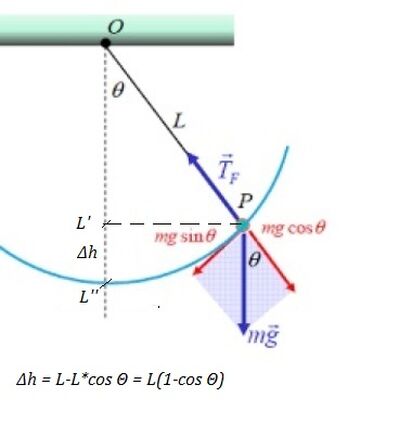
Un pendolo di lunghezza 90 cm oscilla con un angolo massimo di 30◦
rispetto alla verticale. Calcolare la velocità nel punto più basso.
La velocità al punto più basso è: radice quadrata di 2gh.
Quindi per calcolare h: Lcos30° = 0,78 m.
Concludendo la velocità dovrebbe valere 3,91 m/s.
Il fatto è che non sono sicura in merito al calcolo di h e quindi non so se il risultato finale della velocità sia corretto.
104
punti
Livello 0
Non essendoci forze dissipative, tutta l'energia potenziale nel punto di massima elongazione si trasforma in energia cinetica nel punto più basso. Quindi:
mg*DH = 1/2 * m* v²
Da cui si ricava
v= radice (2*g*DH)
Dove:
DH = H(0°) - H(30°) = L*cos(0) - L*cos(30)
L=0,9 m
Sostituendo i valori numerici otteniamo:
v= radice (2,364) = 1,54 m/s
76754
punti
Genius II
@stefanopescetto grazie mille
Figurati! Buona serata
U=m·g·l·(1 - COS(30°))
con U = energia potenziale (nel punto più alto)
che si trasforma in
E = 1/2·m·v^2
con E = energia cinetica (nel punto più basso)
Quindi:
m·g·l·(1 - COS(30°)) = 1/2·m·v^2
con l = 0.9 m; g = 9.806 m/s^2
si ottiene:
m·9.806·0.9·(1 - COS(30°)) = 1/2·m·v^2
da cui: v = 1.54 m/s
94807
punti
Genius II
Un pendolo di lunghezza L = 90 cm oscilla con un angolo massimo di 30◦
rispetto alla verticale. Calcolare la velocità nel punto più basso.
Δh = L*(1-cos 30°) = 0,90*(1-0,866) = 0,121 m
conservazione dell'energia :
V = √2*g*Δh = √19,612*0,121 = 1,54 m/sec
114508
punti
Genius II
@remanzini_rinaldo grazie mille per la spiegazione
