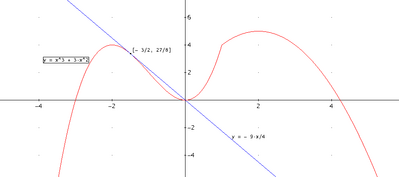
La figura rappresenta il grafico della funzione continua $f(x)$, la retta $t$ tangente in $A$ al grafico di $f(x)$ e la retta $s$ tangente destra in $C$ al grafico di $f(x)$.
a. Determina i valori dei parametri reali $a, b, c$ e $d$ in modo che l'espressione della funzione sia
$$
f(x)= \begin{cases}a x^3+b x^2 & \text { se } x<1 \\ c x^2+d x+1 & \text { se } x \geq 1\end{cases}
$$
b. Trova i punti stazionari della funzione $f(x)$ e verifica che il punto $C$ è angoloso.
c. Determina le coordinate del punto $P$ di ascissa non nulla in cui il grafico di $f(x)$ ha tangente passante per l'origine.
Avrei bisogno della domanda c del numero 69.