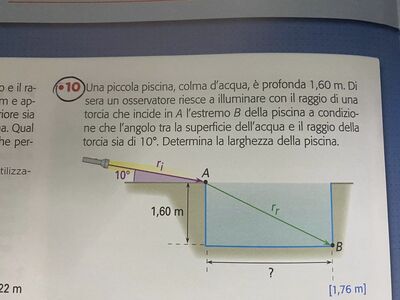
Una piccola piscina, colma d'acqua, è profonda 1,60 m. Di sera un osservatore riesce a illuminare con il raggio di una torcia che incide in $A$ l'estremo $B$ della piscina a condizione che l'angolo tra la superficie dell'acqua e il raggio della torcia sia di $10^{\circ}$. Determina la larghezza della piscina.
buongiorno, qualcuno potrebbe aiutarmi ?
12
punti
Livello 0
@oismen ciao, scusa posso chiederti gentilmente il libro di testo da cui è tratto il problema? grazie mille
Legge di rifrazione:
sen i / sen r = n2 / n1;
i = angolo di incidenza che il raggio di luce forma con la perpendicolare alla superficie di separazione aria acqua.
i = 90° - 10° = 80°
r = angolo di rifrazione.
n2 = 1,33; (indice dell'acqua).
n1 = 1 (indice dell'aria).
sen 80° / sen r = 1,33;
sen r = sen80° / 1,33 = 0,740;
r = sen^-1(0,740) = 47,8°; (angolo di rifrazione).
Lunghezza piscina:
x / h = tan (47,8°);
x = h * tan (47,8°) = 1,60 * 1,103 = 1,76 m.
@oismen ciao
74717
punti
Genius II
Dalla legge di Snell
ni sin ai = nt sin at
1 * sin 100° = 1.33 * sin at
sin at = sin 100° : 4/3 = 3/4 sin 100°
at ~ 47.61°
Infine
x = L sin at
1.6 = L cos at
x/1.6 = tg at
x = 1.6 * tg (47.61°) m = 1.753 m
47869
punti
Livello 7
Dati:
angolo d'incidenza $ϑ_i= 90°-10° = 80°$;
angolo di rifrazione $ϑ_r= ?$;
indice di rifrazione dell'aria $n_i= 1$;
indice di rifrazione dell'acqua $n_r= 1,33$;
applica la legge di Snell con la seguente proporzione:
$sen(ϑ_i) : sen(ϑ_r) = n_r : n_i$
$sen(80°) : sen(ϑ_r) = 1,33 : 1$
$sen(ϑ_r)= \frac{sen(80°)×1}{1,33} ≅ 0,74$
$angolo~ ϑ_r = arcsen(0,74) ≅ 47,73° (arcsen = sen^{-1})$;
infine:
larghezza della piscina $= 1,60×tan(47,73°) ≅ 1,76~m$.
57816
punti
Genius I
