Problema geometrico su quadrilatero

Anch'io ho da premettere qualcosina.
Se non fossi ormai dopo tanti mesi d'interazione più che rassegnato al fatto d'incontrare oggettive difficoltà nell'esprimermi in modo da farmi capire da te a prima lettura, mi sentirei (più che offeso) disprezzato nel leggere che "ci sono oggettive difficoltà interpretative e di soluzione", nonostante la diplomatica frase finale "Ovviamente chi l'ha già fatto ieri, non l'abbia a male.".
Ma come "non l'abbia a male"? Mica mi hai pestato un piede per uno scossone del tram, qui m'hai sputato in faccia deliberatamente e io non dovrei averla a male?
La diplomazia non è mica taumaturgica, a volte dovrà pure arrendersi di fronte all'evidenza dei fatti: è un fatto che tu asserisci prima «ho ricevuto alcune risposte» e, dopo un semplice "ma", «ci sono oggettive difficoltà interpretative e di soluzione»!
------------------------------
Sulla base di quanto t'ho risposto ieri
http://www.sosmatematica.it/forum/postid/88136/
NEGO CHE CI SIANO OGGETTIVE DIFFICOLTÀ DI SOLUZIONE
Il testo che hai pubblicato ieri avrebbe dovuto avere come UNICA RISPOSTA CORRETTA a norma d'esame «Il testo presenta un problema indeterminato perché nomina il punto M senz'averlo definito.».
A seguito di un recente scambio di commenti con @LucianoP sulle tolleranze interpretative da accettare qui su ∫σ∫ ho introdotto l'ipotesi semplificativa "Ammesso che M sia l'incrocio delle diagonali." con la quale la risposta (scorretta a norma d'esame, ma coerente con l'ipotesi introdotta) è diventata «Il testo presenta un problema impossibile perché se ne deduce che un segmento ha lunghezza negativa.».
Dopo una breve meditazione ho introdotto l'ulteriore ipotesi semplificativa "Nel testo c'è un errore di stampa" con la quale (insieme a quella su M) ho definito un problema ben posto del quale ti ho esibito, secondo la tua richiesta, "lo svolgimento dell'esercizio passaggio per passaggio e ... la figura del quadrilatero".
Quindi, di tre problemi ottenuti per approssimazioni successive, ti ho fornito tutt'e tre le risoluzioni e le conseguenti soluzioni corrette: quali sarebbero le "oggettive difficoltà di soluzione"? Ti sfido a sottoporle alla pubblica discussione.
La sola verità che si possa toccare con mano è che «IL TESTO E' ROTONDAMENTE ERRATO».
------------------------------
NEGO ALTRESI' CHE CI SIANO OGGETTIVE DIFFICOLTÀ INTERPRETATIVE
Sull'interpretazione delle mie risposte mi sono già espresso ad abundantiam.
C'è anche una terza risposta pubblicata da @Luix la quale però, avendo scambiato cazzi per lampioni ("Dato che le diagonali del quadrilatero sono perpendicolari, si tratta di un parallelogramma rettangolo."), ha poi conseguentemente applicato il Teorema dello Pseudo-Scoto.
E pure su questa risposta non c'è nulla da interpretare: o t'accorgi che è rotondamente errata o non te n'accorgi.
Anche su questo punto, ti chiedo quali sarebbero le "oggettive difficoltà interpretative"? NON LE TUE, QUELLE OGGETTIVE! Ti sfido a sottoporle alla pubblica discussione.
------------------------------
Come t'ho scritto in premessa, essendo rassegnato al fatto che mi esprimo in forme che non ti sono subito chiare, resto a disposizione per chiarirti qualunque espressione che ti possa sembrare equivoca e ti saluto comunque, anche se non con la consueta serenità di spirito.

Se le diagonali sono perpendicolari, il quadrilatero è un deltoide, se non è un rombo.

M che punto è?

BM ed MD che cosa sono? Possibile che non ti possa spiegare meglio?

Fatti una figura. Così non si capisce niente... Che fatica. ..

Allora sembra che M sia il punto di intersezioni della diagonali: 

BD = 48 cm è una diagonale; BM = MD = 24 cm.

Area = 1200 cm^2;

DM = 24 cm

Il lato CD = 8 + CM;

Applichiamo Pitagora nel triangolo CDM e troviamo CM e il lato CD:

CD^2 = CM^2 + 24^2;

(8 + CM)^2 = CM^2 + 24^2;

64 + CM^2 + 16 CM = CM^2 + 576;

16 CM = 576 - 64;

CM = 512 /16 = 32 cm;

CD = 32 + 8 = 40 cm; (lato maggiore del quadrilatero ABCD);

Consideriamo il deltoide come somma dei due triangoli ABD e BCD con base BD in comune.

Area triangolo BCD = 48 * 32 / 2 = 768 cm^2; (triangolo sotto, in figura);

Area triangolo  ABD = 1200 - 768 = 432 cm^2;

AM = altezza del triangolo ABD; AM = Area * 2 / BD;

AM = 432 * 2 / 48 = 18 cm;

Lato minore BD:

BD = radicequadrata(18^2 + 24^2) = radice(900) = 30 cm; (lato minore);

Perimetro = 30 * 2 + 40 * 2 = 60 + 80 = 140 cm.

Ce l'ho fatta a capire! Che fatica a capire ciò che non ti fanno capire...

Ciao  @beppe

Ciao @beppe

Ciao @beppe non mi pare il caso comunque di screditare i colleghi che rispondono. Comunque penso ci sia un problema con il libro o con il testo che ci hai scritto. Il punto M da dove viene??? Poi BM E MD COSA SONO??? Punti a caso?

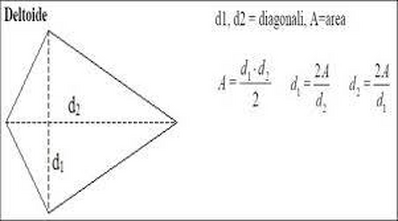
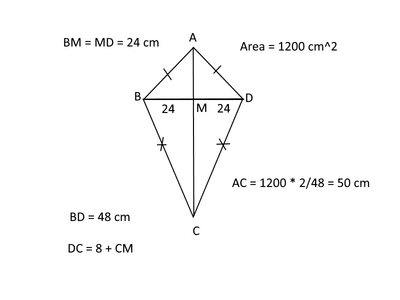
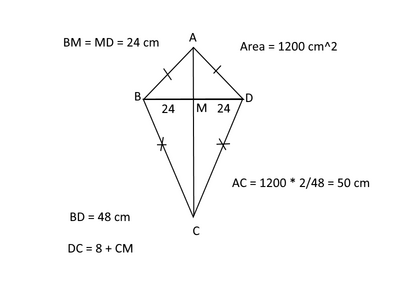
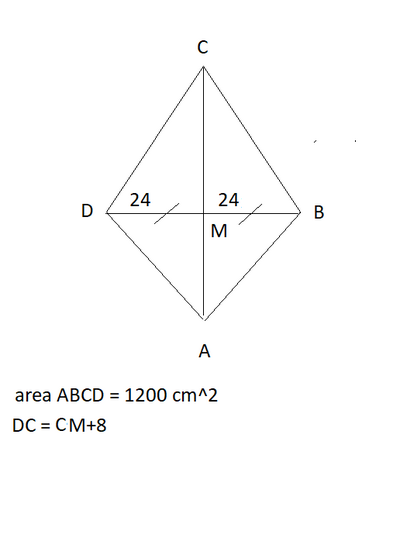
Buona giornata a tutti; premetto che questa è la seconda volta che vado a postare il problema; ieri ho ricevuto alcune risposte, ma ci sono oggettive difficoltà interpretative e di soluzione. Il testo è il seguente : nel quadrilatero ABCD le diagonali sono perpendicolari e si ha BM = MD e BD =  48cm . Si conosce che l'area A del quadrilatero è di 1.200 cm ^2 e che il lato maggiore supera di cm. 8 la sua proiezione ortogonale sulla diagonale AC. Determinare il perimetro del quadrilatero. Risposta cm. 140. Chiederei gentilmente lo svolgimento dell'esercizio passaggio per passaggio e possibilmente la figura del quadrilatero. 

CM^2 +24^2 = (CM+8)^2

24^2 = 8^2+16CM 

CM = (24^2-8^2)/16 = 32

CD = 32+8 = 40

AC = 2A/48 = 50 cm 

AD = √24^2+18^2 = √24^2+18^2 = 30

perimetro 2p = (30+40)*2 = 140,0 cm