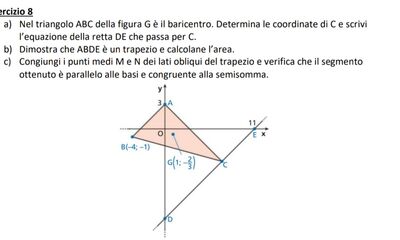
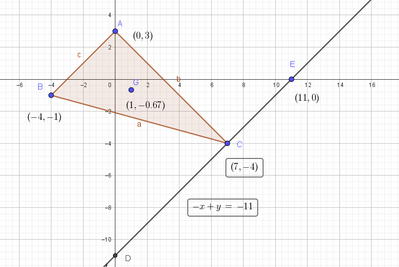
Nel triangolo $A B C$ della figura $G$ è il baricentro. Determina le coordinate di $C$ e scrivi l'equazione della retta $D E$ che passa per $C$.
Dimostra che ABDE è un trapezio e calcolane l'area.
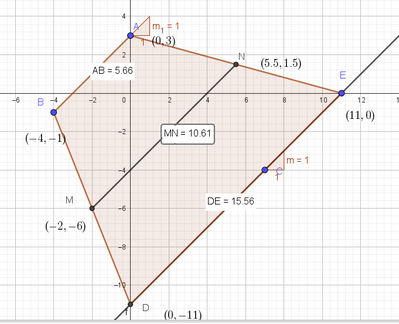
Congiungi i punti medi $\mathrm{M}$ e $\mathrm{N}$ dei lati obliqui del trapezio e verifica che il segmento ottenuto è parallelo alle basi e congruente alla semisomma.
Ciao a tutti,
Avrei bisogno di un aiuto per la risoluzione del punto C dell'esercizio allegato, grazie 🙂
130
punti
Livello 1
* G = (A + B + C)/3 = ((0, 3) + (- 4, - 1) + (x, y))/3 = ((x - 4)/3, (y + 2)/3) = (1, - 2/3) ≡
≡ ((x - 4)/3 = 1) & ((y + 2)/3 = - 2/3) ≡
≡ (x = 7) & (y = - 4) ≡
≡ C(7, - 4)
---------------
* E(11, 0)
* CE ≡ y = x - 11
* (x = 0) & (y = x - 11) ≡ D(0, - 11)
* |DE| = 11*√2
---------------
* AB ≡ y = x + 3
* |AB| = 4*√2
--------
Che AB e CE abbiano entrambe pendenza uno ne dimostra il parallelismo e l'altezza h del trapezio ABDE è il lato del quadrato che ha per diagonale la distanza fra le loro intercette
* h = (11 + 3)/√2 = 7*√2
da cui l'area
* S(ABDE) = h*(|AB| + |DE|)/2 = (7*√2)*(4*√2 + 11*√2)/2 = 105
---------------
* M = (B + D)/2 = ((- 4, - 1) + (0, - 11))/2 = (- 2, - 6)
* N = (A + E)/2 = ((0, 3) + (11, 0))/2 = (11/2, 3/2)
* MN ≡ y = x - 4 (anch'essa di pendenza uno)
* |MN| ≡ 15/√2 = (|AB| + |DE|)/2 = (4*√2 + 11*√2)/2 ≡ Vero
57382
punti
Genius I
@exprof La ringrazio, buona serata 🙂
