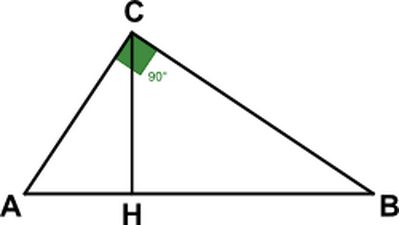
In un triangolo rettangolo i due cateti misurano rispettivamente $60 \mathrm{~cm} \mathrm{e} 45 \mathrm{~cm}$. Calcola Yarea e il perimetro del triangolo sapendo che il cateto minore supera di $9 \mathrm{~cm}$ l'altezza relativa all'ipotenusa.
$\left(1350 \mathrm{~cm}^2 ; 180 \mathrm{~cm}\right)$
Problema, numero 205
14
punti
Livello 0
3606
punti
Livello 5
Area = b * h / 2.
I cateti sono uno base e uno altezza; quindi l'area si trova moltiplicando i cateti AC e CB in figura e dividendo per 2.
A = AC * CB / 2 ;
A = 60 * 45 / 2 = 1350 cm^2; (area triangolo),
AB è l'ipotenusa; CH è la sua altezza relativa;
AC = CH + 9 cm;
AC = 45 cm
CH = 45 - 9 = 36 cm; altezza relativa all'ipotenusa;
L'area si trova anche facendo:
AB * CH / 2 = Area ;
AB * 36 / 2 = 1350;
AB = 1350 * 2 / 36 = 75 cm; (ipotenusa AB);
Perimetro = 75 + 45 + 60 = 180 cm.
Ciao @loretafloreno
Metti le figure diritte!
74150
punti
Genius II
Non leggo di traverso: trascrivi su tastiera, cavolo!
http://www.sosmatematica.it/forum/postid/99968/
e leggiti bene il
http://www.sosmatematica.it/regolamento/
57363
punti
Genius I
