Problema funzione lineare

Question

Un ricco signore vuole ormeggiare durante la stagione estiva il suo panfilo per un certo periodo di tempo in un porticciolo gestito da un club nautico. Ha le seguenti possibilità:
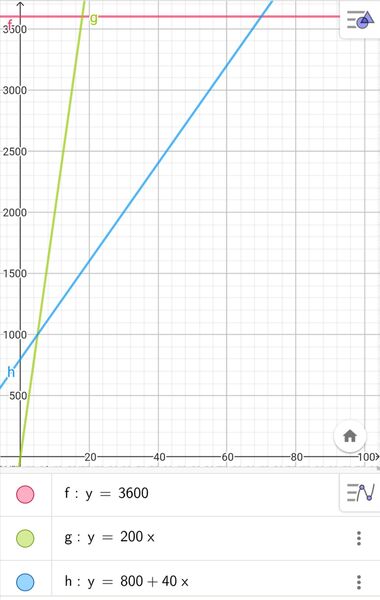
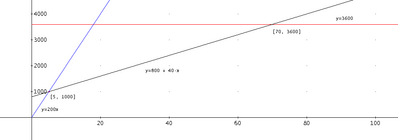
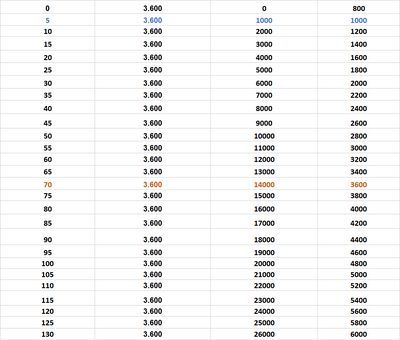
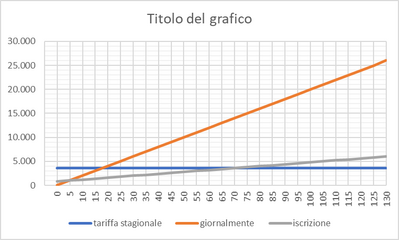
- prendere in affitto il posto barca per l'intera stagione estiva (dal primo giugno al 30 settembre), pagando 3600 euro;
- pagare la tariffa di ormeggio di 200 euro al giorno;
- iscriversi al club, pagando una quota di iscrizione di 800 euro, quindi pagare la tariffa di ormeggio agevolata, di 40 euro al giorno.
Stabilisci qual è la scelta più conveniente, in relazione al numero dei giorni di ormeggio.

Buonasera, vorrei sapere come svolgere al meglio questo problema sulle funzioni lineari.

Grazie mille

Autore

Risposta

EnjaS

(@enjas)

263 punti

livello:

Livello 1

97 Risposte
73 0 24

09/12/2022 16:24

StefanoPescetto · Accepted Answer

[attach]31710[/attach] Nei primi 5 gg la scelta migliore è pagare quotidianamente €200. Indicando con x= numero di giorni  {y= 200*x {y= 800 + 40*x   => x= 5 gg   Al 5gg i due costi sono equivalenti.  È indifferente aver pagato quotidianamente o aver pagato la quota d'iscrizione e la tariffa giornaliera agevolata.    Dal 6 gg al 69-esimo conviene pagare la quota d'iscrizione e la tariffa giornaliera agevolata.  {y = 3600 {y = 800 + 40*x  => x=70 gg   Al 70 gg i due costi sono equivalenti.  È indifferente aver pagato la quota d'iscrizione e la tariffa giornaliera agevolata oppure aver pagato per l'intera stagione estiva.    Dal 71-esimo gg conviene pagare l'intera quota per la stagione, pari a €3600.

mg · Answer

Giorni di ormeggio (4 mesi):

30 (giugno) + 31 (luglio) + 31 (agosto) + 30 (settembre);

numero giorni x:

x = 122 giorni;

y = costo.

1) y = 3600 €; (costo affitto per l'intera stagione).

2) y = 200 * x;

y = 200 * 122 = 24400 €;

3) y = 40 * x + 800;

y = 40 * 122 + 800 = 5680 €;

Meglio la prima opzione: pagare l'affitto.

Per qualche giorno conviene la 2) o la 3);

200 x < 40 x + 800 ;

160 x < 800;

x < 5; per x < 5 conviene la 2).

Per 4 giorni si spendono 2 * 4 = 800 €, come il costo dell'abbonamento.

Ciao @enjas

mg

(@mg)

74869 punti

livello:

Genius II

10660 Risposte
5 4834 1556

09/12/2022 16:59

LucianoP · Answer

[attach]31713[/attach] La scelta è indifferente in corrispondenza dei punti segnati sul grafico. Precisamente : {y = 200·x {y = 800 + 40·x che porta al punto [x = 5 gg ∧ y = 1000 €] {y = 800 + 40·x {y = 3600 che porta al punto [x = 70 gg ∧ y = 3600 €] Quindi la tariffa y = 200·x per un numero di giorni x<5 gg la tariffa y = 800 + 40·x per x: 5<=x<70 gg per x>=70 gg la tariffa di 3600

remanzini_rinaldo · Answer

[attach]31851[/attach] [attach]31850[/attach] da zero a 5 gg è più vantaggiosa la tariffa giornaliera da 6 a 70 gg è più vantaggiosa l'iscrizione al club nautico da 71gg on è più vantaggiosa la piena tariffa stagionale

[Risolto] Problema funzione lineare

Domande