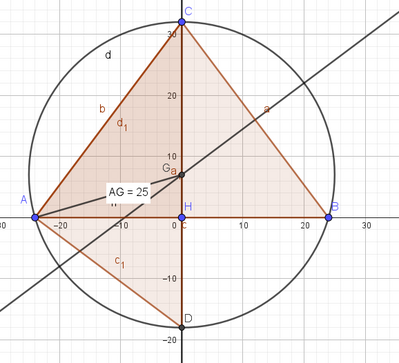
Un triangolo isoscele ha base AB e altezza CH, con AB + CH =80 e AB > CH; l'area è di 768 cm².
a. Trova il raggio della circonferenza circoscritta al triangolo (SUGGERIMENTO Prolunga l'altezza CH fino incontrare la circonferenza in D e considera poi il triangolo ACD...)
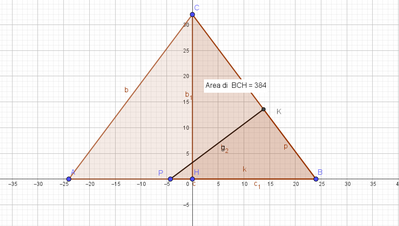
b. Considera P su HB e traccia la perpendicolare PK a CB. Determina per quale posizione di P il triangolo PKB ha area uguale a 192 cm².
SOLUZIONI
[a) 25 cm; b) PB=20*radice quadrata di 2 cm]
8
punti
Livello 0
ΑΒ = x
CH = y
x > y
{x + y = 80
{1/2·x·y = 768
Sistema simmetrico che ammette soluzione: [x = 32 ∧ y = 48, x = 48 ∧ y = 32]
Quindi deve essere: x = 48 cm ∧ y = 32 cm
Quindi facendo riferimento alla figura allegata, considero il triangolo rettangolo ACD retto in A:
ΑΗ = 48/2 = 24 cm = altezza relativa all'ipotenusa CD= diametro della circonferenza circoscritta
Vale il 2° teorema di Euclide per cui si ha:
AH^2=CH*HD-----> HD=AH^2/CH=24^2/32 = 18 cm
Da cui il raggio r:
r = AG=(CH+HD)/2=(32+18)/2= 25 cm
--------------------------------------------
Ultima domanda...
Fai riferimento ai triangoli rettangoli simili: CHB e PKB
Ti serve la distanza PB che è ipotenusa del triangolo PKB
Fai il rapporto delle due aree:
A(CHB)=768/2 = 384 cm^2 ; A(PKB)=192 cm^2
384/192 = 2
Quindi significa che il rapporto fra le due ipotenuse debba valere √2
Quindi : BC=√(24^2 + 32^2) = 40 cm
da cui PB=40/√2 = 20·√2
94597
punti
Genius II
