Ho questo problema:
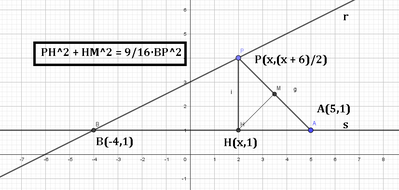
Data la retta r di equazione x-2y+6=0 e il punto A (5;1), sia B il punto in cui r incontra la retta s per A parallela all'asse delle ascisse e P un generico punto su r. Indicato con M il punto medio AP e con H la proiezione di P su s, determinare la posizione di P affinchè
PH^2+HM^2=9/16BP^2
308
punti
Livello 1
Intanto disegno su cui ragionare:
PH^2=((x + 6)/2 - 1)^2 = (x + 4)^2/4
Punto medio M:
{x = (x + 5)/2
{y = ((x + 6)/2 + 1)/2 = (x + 8)/4
Quindi: M[(x + 5)/2, (x + 8)/4]
HM^2= ((x + 5)/2 - x)^2 + ((x + 8)/4 - 1)^2 = (5·x^2 - 32·x + 116)/16
Altro quadrato a secondo membro della figura:
BP^2=(x + 4)^2 + ((x + 6)/2 - 1)^2 = 5·(x + 4)^2/4
Quindi si tratta di risolvere:
(x + 4)^2/4 + (5·x^2 - 32·x + 116)/16 = 9/16·(5·(x + 4)^2/4)
se lo fai tu, con un po' di buona volontà: x = -40 ∨ x = 0
Quindi i due punti P sulla retta sono:
[-40, (-40 + 6)/2] = [-40, -17]
[0, (0 + 6)/2] = [0, 3]
94710
punti
Genius II
Si il disegno sono riuscita a farlo e mi sono calcolata anche il punto B e la retta che passa per il punto A parallela all'asse delle x.
Perché sta su r, e l'equazione esplicita di questa é 2y = x + 6 => y = (x+6)/2
Si,si, è vero.
@lucianop Grazie mille. Sei stato gentilissimo! 😊
