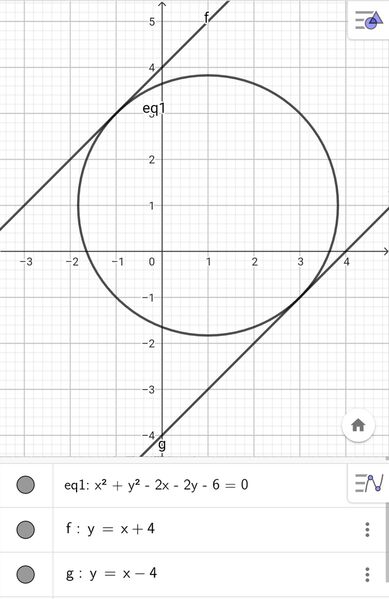
Non ho capito questo esercizio di geometria analitica sulla circonferenza mi potreste aiutare.
Determina le equazioni delle rette parallele alla bisettrice del primo e del terzo quadrante e tangenti alla circonferenza di equazione x^2+ y^2-2x-2y-6.
Mi potreste fare anche i calcoli