Ciao a tutti non riesco proprio a fare questo esercizio riuscireste ad aiutarmi? Ringrazio in anticipo chi lo farà.
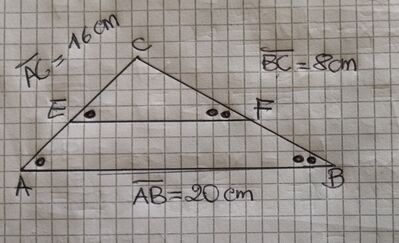
Un triangolo ABC ha perimetro di 44cm, AB è lungo 20cm e AC è lungo 16cm. Una retta parallela ad AB taglia i lati AC e BC rispettivamente in E e F ed è tale che CF=3cm. Calcola la lunghezza di AE.