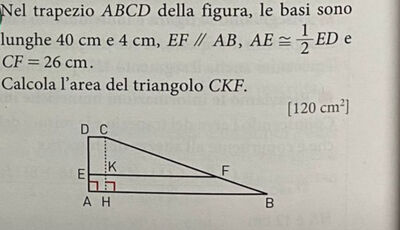
Nel trapezio $A B C D$ della figura, le basi sono lunghe $40 \mathrm{~cm} \mathrm{e} 4 \mathrm{~cm}, E F / / A B, A E \cong \frac{1}{2} E D \mathrm{e}$ $C F=26 \mathrm{~cm}$.
Calcola l'area del triangolo $C K F$.
$$
\left[120 \mathrm{~cm}^2\right]
$$
Ciao! Potete aiutarmi a risolvere questo problema? Grazie.
116
punti
Livello 1
DA : DE = CB : CF; (teorema di Talete)
DA = DE + EA = DE + 1/2 DE;
DA = 3/2 DE;
DA : DE = 3/2;
3 : 2 = CB : 26;
CB = 26 * 3 / 2 = 39 cm; lato obliquo del trapezio
HB = 40 - 4 = 36 cm;
CH = radicequadrata(39^2 - 36^2) = radice(225) = 15 cm; (altezza del trapezio e del triangolo CHB);
CH = DA;
CK = 2 KH ;
CK + KH = 15 cm;
2 KH + KH = 15;
KH = 15 / 3 = 5 cm;
CK = 2 * KH = 10 cm; altezza del triangolo CKF,
Triangoli simili CKF; CHB
KF : HB = CF : CB;
KF : 36 = 26 : 39;
KF = 26 * 36 / 39 = 24 cm ; (base del triangolo CKF);
Area CKF = 24 * 10 / 2 = 120 cm^2.
Ciao @elenafrattini
74887
punti
Genius II
